K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7 tháng 11 2021
a) \(\Rightarrow\left|\dfrac{3}{4}+x\right|=0\Rightarrow\dfrac{3}{4}+x=0\Rightarrow x=-\dfrac{3}{4}\)
b) \(\Rightarrow x+0,4=\dfrac{4}{9}:\dfrac{2}{3}=\dfrac{2}{3}\Rightarrow x=\dfrac{2}{3}-0,4=\dfrac{4}{15}\)
7 tháng 11 2021
\(=\left(\dfrac{7}{4}.\dfrac{2}{7}\right).\dfrac{4}{5}=\dfrac{1}{2}.\dfrac{4}{5}=\dfrac{2}{5}\)
7 tháng 11 2021
a/\(\left(1,75:\dfrac{7}{2}\right).\dfrac{4}{5}=\left(\dfrac{7}{4}:\dfrac{7}{2}\right).\dfrac{4}{5}=\dfrac{1}{2}.\dfrac{4}{5}\dfrac{2}{5}\)
7 tháng 11 2021
Bài 1:
\(a,A=\dfrac{22}{7}-\dfrac{22}{7}-0,25-0,75-4=-1-4=-5\\ b,B=\dfrac{1\cdot\left(\dfrac{2}{5}\right)^3\cdot\left(\dfrac{15}{4}\right)^2}{\left(\dfrac{15}{2^2}\right)^2\cdot\left(\dfrac{2}{5}\right)^3}=1\)
Bài 2:
\(a,\Rightarrow2^{x+3}=13,9+2,1=16=2^4\\ \Rightarrow x+3=4\Rightarrow x=1\\ b,\Rightarrow\left|x-\dfrac{3}{2}\right|=0,5=\dfrac{1}{2}\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}+\dfrac{3}{2}=2\\x=-\dfrac{1}{2}+\dfrac{3}{2}=1\end{matrix}\right.\\ c,\Rightarrow\dfrac{x}{2}=\dfrac{y}{7}=\dfrac{2x-5y}{2\cdot2-5\cdot7}=\dfrac{93}{-31}=-3\\ \Rightarrow\left\{{}\begin{matrix}x=-6\\y=-21\end{matrix}\right.\)
6 tháng 11 2021
b: \(\Leftrightarrow x+\dfrac{2}{5}=\dfrac{2}{3}\)
hay \(x=\dfrac{1}{15}\)
DM
1
AH
Akai Haruma
Giáo viên
12 tháng 8 2023
Lời giải:
a. Với $n$ nguyên khác -3, để $B$ nguyên thì:
$2n+9\vdots n+3$
$\Rightarrow 2(n+3)+3\vdots n+3$
$\Rightarrow 3\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{-2; -4; 0; -6\right\}$
b.
$B=\frac{2n+9}{n+3}=\frac{2(n+3)+3}{n+3}=2+\frac{3}{n+3}$
Để $B_{\max}$ thì $\frac{3}{n+3}$ max
Điều này đạt được khi $n+3$ là số nguyên dương nhỏ nhất
Tức là $n+3=1$
$\Leftrightarrow n=-2$
c. Để $B$ min thì $\frac{3}{n+3}$ min
Điều này đạt được khi $n+3$ là số nguyên âm lớn nhất
Tức là $n+3=-1$
$\Leftrightarrow n=-4$
NT
0
19 tháng 2 2022
Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)
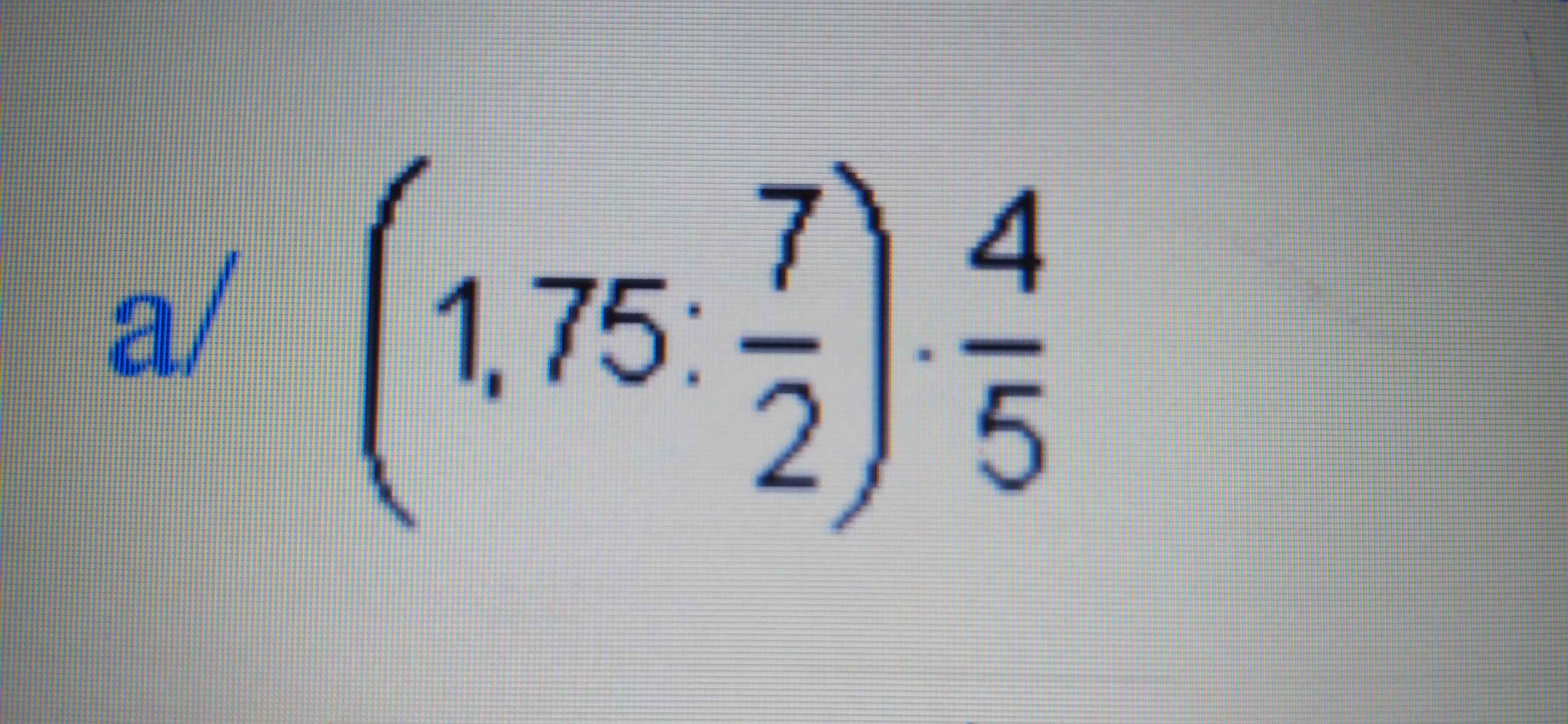
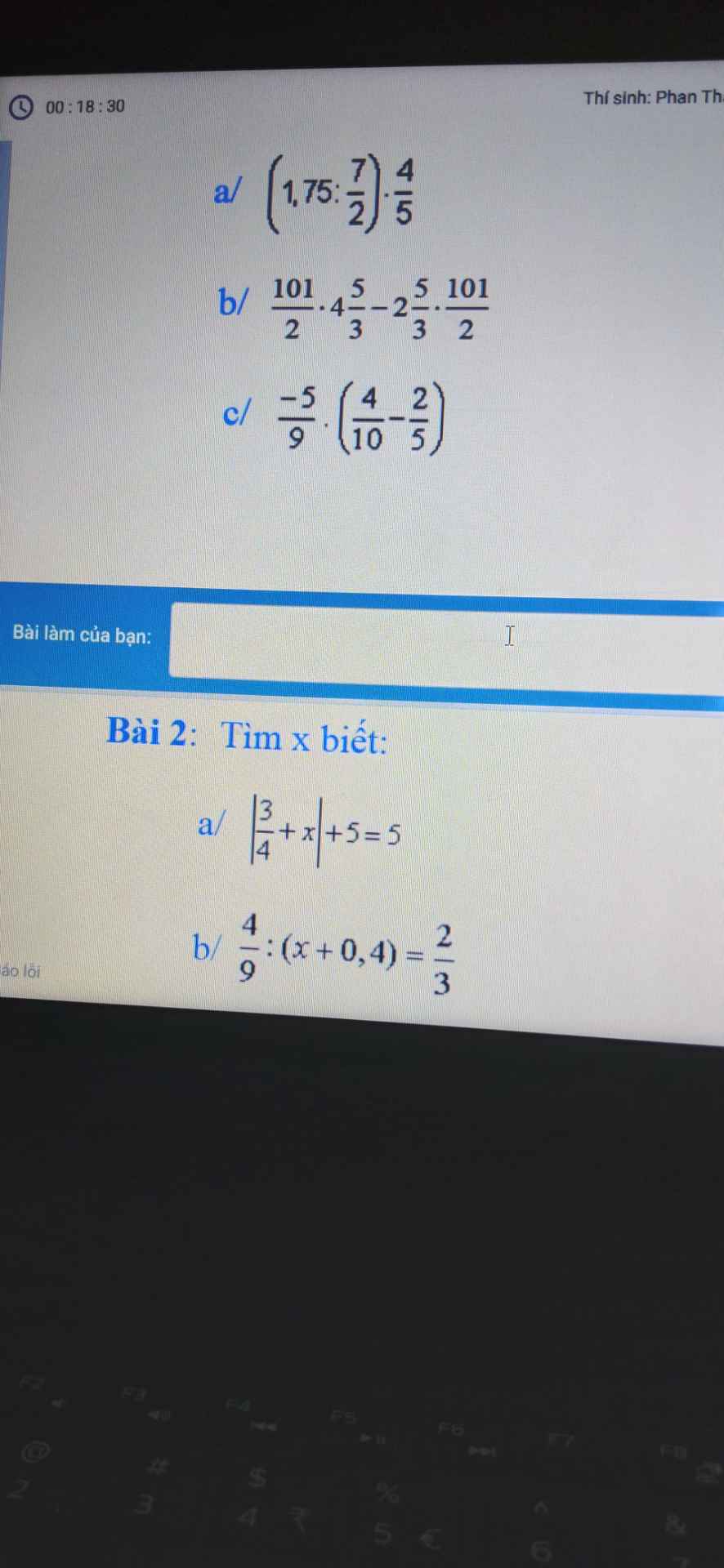
\(=\dfrac{101}{2}\left(4+\dfrac{5}{3}-2-\dfrac{5}{3}\right)=\dfrac{101}{2}\cdot2=101\)