
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(e,\left(x-2\right)^2-16=0\\ \Leftrightarrow\left(x-6\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\\ f,x^2-5x-14=0\\ \Leftrightarrow\left(x-7\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=7\\x=-2\end{matrix}\right.\\ g,8x\left(x-3\right)+x-3=0\\ \Leftrightarrow\left(8x+1\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{8}\\x=3\end{matrix}\right.\)

Lần sau bạn chú ghi đầy đủ đề. Tìm $k$ để $f(x)$ chia hết cho........ nhé.
Lời giải:
a. Áp dụng định lý Bê-du về phép chia đa thức, để $f(x)$ chia hết cho $g(x)=x-2$ thì:
$f(2)=0$
$\Leftrightarrow 2^3+2.2^2-k+8=0\Leftrightarrow k=8$
b. Áp dụng định lý Bê-du về phép chia đa thức, để $f(x)$ chia hết cho $g(x)=x+4$ thì:
$f(-4)=0$
$\Leftrightarrow (-4)^3+2(-4)^2-k+8=0$
$\Leftrightarrow -24-k=0$
$\Leftrightarrow k=-24$

c: \(=\dfrac{15x+9+\left(x-9\right)\left(x+3\right)}{3\cdot\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{15x+8+x^2-6x-27}{3\left(x-3\right)\left(x+3\right)}=\dfrac{x^2+9x-19}{3\left(x-3\right)\left(x+3\right)}\)

\(e,\left(x^3+3x^2y-2xy^2\right)\left(-3x^2y\right)\)
\(=\left(-3x^2.x^3.y\right)+\left(-3x^2y.3x^2y\right)+\left(-3x^2y.\left(-2xy^2\right)\right)\)
\(=-3x^5y-9x^4y^2+6x^3y^3\)
\(f,\left(4x^2-\dfrac{3}{2}xy+\dfrac{1}{4}\right)\left(-10xy^2\right)\)
\(=\left(-10xy^2.4x^2\right)+\left(-10xy^2.\left(-\dfrac{3}{2}xy\right)\right)+\left(-10xy^2.\dfrac{1}{4}\right)\)
\(=-40x^3y^2+15x^2y^3-\dfrac{5}{2}xy^2\)

\(f,\Leftrightarrow x^3+2x^2+5x-2x^2-4x-10+2\left(x^2-4\right)-5x+10=0\\ \Leftrightarrow x^3-4x+2x^2-8=0\\ \Leftrightarrow x^3+2x^2-4x-8=0\\ \Leftrightarrow x^2\left(x-2\right)-4\left(x-2\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x-2\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)

b: ĐKXĐ: x<>-3
\(\dfrac{3x+x^2}{x^2+x+1}\cdot\dfrac{3x^3-3}{x+3}\)
\(=\dfrac{x\left(x+3\right)}{x^2+x+1}\cdot\dfrac{3\left(x^3-1\right)}{x+3}\)
\(=\dfrac{3x\left(x-1\right)\left(x^2+x+1\right)}{x^2+x+1}=3x\left(x-1\right)\)
e: ĐKXĐ: \(x\notin\left\{4;-5\right\}\)
\(\dfrac{2x+10}{x^3-64}:\dfrac{\left(x+5\right)^2}{2x-8}\)
\(=\dfrac{2\left(x+5\right)}{\left(x-4\right)\left(x^2+4x+16\right)}\cdot\dfrac{2x-8}{\left(x+5\right)^2}\)
\(=\dfrac{2\cdot2\left(x-4\right)}{\left(x-4\right)\left(x^2+4x+16\right)}=\dfrac{4}{x^2+4x+16}\)





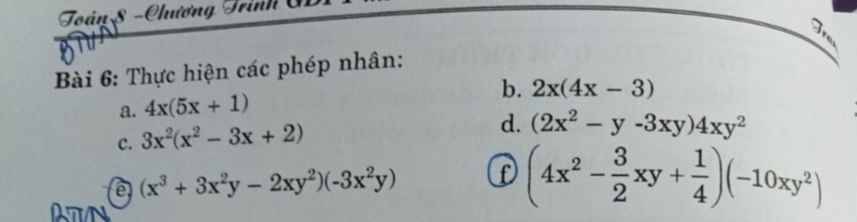
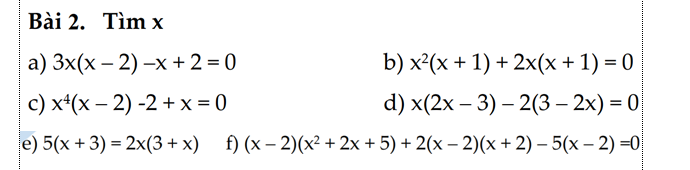 giúp mik câu f vs ạ
giúp mik câu f vs ạ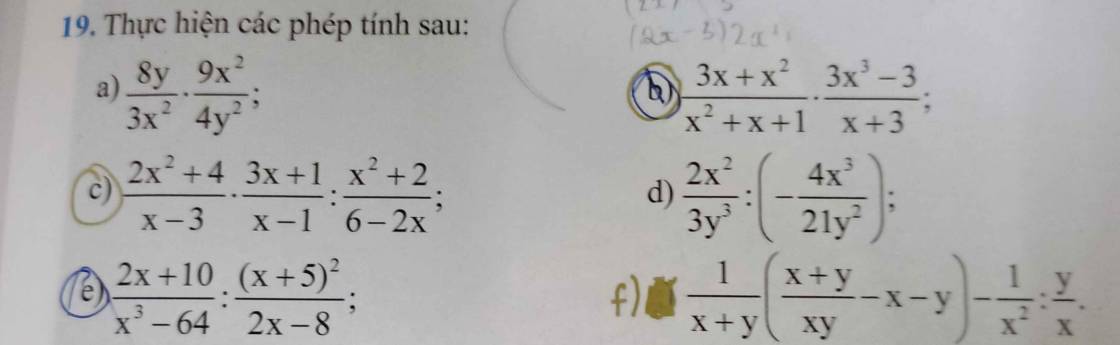
\(f,f\left(x\right)⋮g\left(x\right)\\ \Leftrightarrow4x^4-13x^3+23x^2+18x-k=\left(x+4\right)\cdot c\left(x\right)\)
Thay \(x=-4\left(\text{Bổ đề Bézout}\right)\)
\(\Leftrightarrow4\cdot\left(-4\right)^4-13\cdot\left(-4\right)^3+23\cdot\left(-4\right)^2+18\left(-4\right)-k=0\\ \Leftrightarrow1024+832+368-72-k=0\\ \Leftrightarrow k=2152\)
\(d,f\left(x\right)⋮g\left(x\right)\\ \Leftrightarrow x^4-8x^3+24x^2+7x+k=\left(x+4\right)\cdot a\left(x\right)\)
Thay \(x=-4\left(\text{Bổ đề Bézout}\right)\)
\(\Leftrightarrow\left(-4\right)^4-8\left(-4\right)^3+24\left(-4\right)^2+7\left(-4\right)+k=0\\ \Leftrightarrow256+512+384-28+k=0\\ \Leftrightarrow k=-1124\)