Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Trên đoạn thẳng nối S 1 S 2 hai điểm gần nhau nhất mà phần tử nước tại đó dao động với biên độ cực đại cách nhau d = λ 2 = 3 c m .

Khoảng cách giữa hai cực đại hoặc hai cực tiểu liền kề trên đường nối hai nguồn là: d = λ 2 = 3 c m => Chọn C

Chọn đáp án C
? Lời giải:
+ Khoảng cách giữa hai cực đại hoặc hai cực tiểu liền kề trên đường nối hai nguồn là: λ = d 2 = 3 c m

Đáp án A
Giả sử hai nguồn có cùng phương trình dao động: u = A coswt. Khi đó phương trình dao động tổng hợp tại M là:
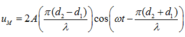
Để M có biên độ cực đại thì: d 2 - d 1 = kl, mà - S 1 S 2 < d 2 - d 1 < S 1 S 2 và S 1 S 2 = 5,6l.
Từ đó:
-5,6l < kl < 5,6l Þ k = 0, ±1, ±2, ±3, ±4, ± 5: có 11 vị trí
Để M dao động cùng pha với 2 nguồn thì: d 2 - d 1 = kl và d 2 + d 1 = k’l > S 1 S 2 = 5,6l (M nằm ngoài S 1 S 2 ). (k và k’ cùng chẵn hoặc cùng lẻ) Vì M nằm gần S 1 S 2 nhất nên khoảng cách ( d 2 + d 1 ) ngắn nhất: d 2 + d 1 =6l; d 2 - d 1 = 4l nên:
d 1 = l; d 2 = 5l
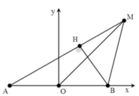
Khoảng cách ngắn nhất giữa M và S 1 S 2 là MH, với:
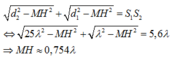

Chọn đáp án D.
Không mất tính tổng quát giả sử λ = 1.
Ta có:
Vì trên AB có 11 vị trí cực đại nên suy ra 5 < λ < 6.
(Dựa vào các đáp án suy ra chỉ có 5,3λ thỏa mãn).

Đáp án A
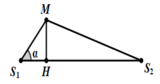
Để M cực đại và cùng pha với 2 nguồn thì
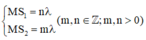
Xét tam giác MS1S2
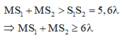
Để M gần S1S2 nhất thì m + n phải nhỏ nhất và m gần S1 nhất => m = 5, n = 1
Có
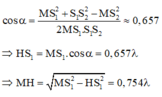

Đáp án A
Các cực đại giao thoa tạo thành các dãy hypebol theo phương trình:
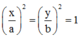
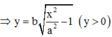
Trong đó
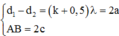
và
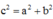
Trong hệ trục tọa độ đã chọn d có phương trình y = x
Gọi N là điểm cực đại trên d gần O nhất, khi đó N thuộc cực đại ứng với k=0
Ta có:
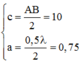
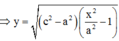
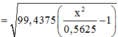
Phương trình gia điểm giữa d và y: y = x
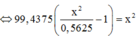
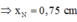
Gọi M là điểm cực đại trên d xa N nhất, khi M tiến về vô cùng thì
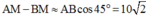
Xét tỉ số
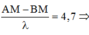
M xa N nhất thuộc cực đại ứng với k=4 → a = 6,75cm
Tương tự ta có phương trình
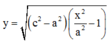
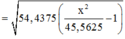
Phương trình gia điểm giữa d và y: y = x
![]()
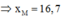
→ Khoảng cách giữa M và N:
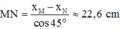



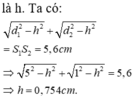
Đáp án C
Khoảng cách gần nhất giữa hai điểm dao động cực đại: