Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ĐKXD: x ≠ 2
\(\dfrac{1}{x-2}+3=\dfrac{3-x}{x-2}\)
\(\Leftrightarrow\dfrac{1}{x-2}-\dfrac{3-x}{x-2}=-3\)
\(\Leftrightarrow\dfrac{1-3+x}{x-2}=-3\)
\(\Leftrightarrow\dfrac{-2+x}{x-2}=-3\)
\(\Leftrightarrow-2+x=-3\left(x-2\right)\)
\(\Leftrightarrow-2+x=-3x+6\)
\(\Leftrightarrow x+3x=6+2\)
\(\Leftrightarrow4x=8\)
\(\Leftrightarrow x=2\) (loại vì không thỏa mãn điều kiện)
Vậy S = ∅
b) ĐKXĐ: x ≠ 7
\(\dfrac{8-x}{x-7}-8=\dfrac{1}{x-7}\)
\(\Leftrightarrow\dfrac{8-x}{x-7}-\dfrac{1}{x-7}=8\)
\(\Leftrightarrow\dfrac{7-x}{x-7}=8\)
\(\Leftrightarrow-1=8\left(vô-lý\right)\)
Vậy S = ∅
P/s: Ko chắc ạ!
c) ĐKXĐ: x ≠ 1
\(\dfrac{1}{x-1}+\dfrac{2x}{x^2+x+1}=\dfrac{3x^2}{x^3-1}\)
Quy đồng và khử mẫu ta được:
\(x^2+x+1+2x\left(x-1\right)=3x^2\)
\(\Leftrightarrow x^2+x+1+2x^2-2x-3x^2=0\)
\(\Leftrightarrow-x+1=0\)
\(\Leftrightarrow x=1\) (loại vì ko t/m đk)
Vậy S = ∅

\(a.\Leftrightarrow\frac{5x^2+16}{\left(x+4\right)\left(x-4\right)}=\frac{\left(2x-1\right)\left(x-4\right)+\left(3x-1\right)\left(x+4\right)}{\left(x+4\right)\left(x-4\right)}DKXD:x\ne4;-4\)
\(\Rightarrow5x^2+16=2x^2-8x-x+4+3x^2+12x-x-4\)
\(\Leftrightarrow2x=16\)
\(\Leftrightarrow x=8\)
\(b.\Leftrightarrow\frac{\left(y+1\right)\left(y+2\right)-5\left(y-2\right)}{\left(y-2\right)\left(y+2\right)}=\frac{12+\left(y-2\right)\left(y+2\right)}{\left(y-2\right)\left(y+2\right)}.DKXD:y\ne2;-2\)
\(\Rightarrow y^2+2y+y+2-5y+10=12+y^2-4\)
\(\Leftrightarrow-2y=-4\)
\(\Leftrightarrow y=2\)

ĐKXĐ: y<>0
\(y^2\left[\dfrac{1}{y\left(y-1\right)+1}-\dfrac{1}{y\left(y+1\right)+1}\right]=\dfrac{3}{y\left(y^4+y^2+1\right)}+\dfrac{2y-2}{y^2-y+1}\)
=>\(y^2\cdot\dfrac{y\left(y+1\right)+1-y\left(y-1\right)-1}{\left(y^2-y+1\right)\left(y^2+y+1\right)}=\dfrac{3}{y\left(y^2-y+1\right)\left(y^2+y+1\right)}+\dfrac{2y-2}{y^2-y+1}\)
=>\(y^2\cdot\dfrac{y\left(y+1-y+1\right)}{\left(y^2-y+1\right)\left(y^2+y+1\right)}=\dfrac{3+\left(2y-2\right)\cdot y\left(y^2+y+1\right)}{y\left(y^2-y+1\right)\left(y^2+y+1\right)}\)
=>\(y^2\cdot\dfrac{y\cdot2\cdot y}{\left(y^2-y+1\right)\cdot\left(y^2+y+1\right)\cdot y}=\dfrac{3+2y\left(y-1\right)\left(y^2+y+1\right)}{y\left(y^2-y+1\right)\left(y^2+y+1\right)}\)
=>\(2y^2\cdot y^2=3+2y\left(y^3-1\right)\)
=>\(2y^4=3+2y^4-2y\)
=>3-2y=0
=>2y=3
=>\(y=\dfrac{3}{2}\left(nhận\right)\)

a) Ta có: \(\dfrac{3x^2-12x+12}{x^2-4}\)
\(=\dfrac{3\left(x^2-4x+4\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{3\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{3\left(x-2\right)}{x+2}\)
\(=\dfrac{3\cdot\left(\dfrac{-1}{4}-2\right)}{\dfrac{-1}{4}+2}=-\dfrac{27}{7}\)
b) Ta có: \(\dfrac{x^2-5x-6}{x^2-9}\)
\(=\dfrac{\left(x-6\right)\left(x+1\right)}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{\left(-1-6\right)\left(-1+1\right)}{\left(-1-3\right)\left(-1+3\right)}\)
=0

1:
a: =>28x-8=9x+3
=>19x=11
=>x=11/19
b: =>(3x-1)(x-1)=(2x+1)(x+1)
=>3x^2-4x+1=2x^2+3x+1
=>x^2-7x=0
=>x=0 hoặc x=7

Lời giải
a)
\(\left(\frac{3}{2x-y}-\frac{2}{2x+y}-\frac{1}{2x-5y}\right).\frac{4x^2-y^2}{y^2}\)
\(=\frac{3(4x^2-y^2)}{(2x-y)y^2}-\frac{2(4x^2-y^2)}{(2x+y)y^2}-\frac{4x^2-y^2}{(2x-5y)y^2}\)
\(=\frac{3(2x-y)(2x+y)}{(2x-y)y^2}-\frac{2(2x-y)(2x+y)}{(2x+y)y^2}-\frac{4x^2-y^2}{(2x-5y)y^2}\)
\(=\frac{3(2x+y)-2(2x-y)}{y^2}-\frac{4x^2}{(2x-5y)y^2}+\frac{1}{2x-5y}\)
\(=\frac{2x+5y}{y^2}-\frac{4x^2}{(2x-5y)y^2}+\frac{1}{2x-5y}\)
\(=\frac{(2x+5y)(2x-5y)-4x^2}{(2x-5y)y^2}+\frac{1}{2x-5y}\)
\(=\frac{4x^2-25y^2-4x^2}{(2x-5y)y^2}+\frac{1}{2x-5y}=\frac{-25}{2x-5y}+\frac{1}{2x-5y}=\frac{-24}{2x-5y}\)
Ta có đpcm.
b)
\(\frac{x^2-x+1}{x^2+x}.\frac{x+1}{3x-2}.\frac{9x-6}{x^2-x+1}\)
\(=\frac{(x^2-x+1)(x+1).3(3x-2)}{x(x+1)(3x-2)(x^2-x+1)}\)
\(=\frac{3}{x}\) (đpcm)
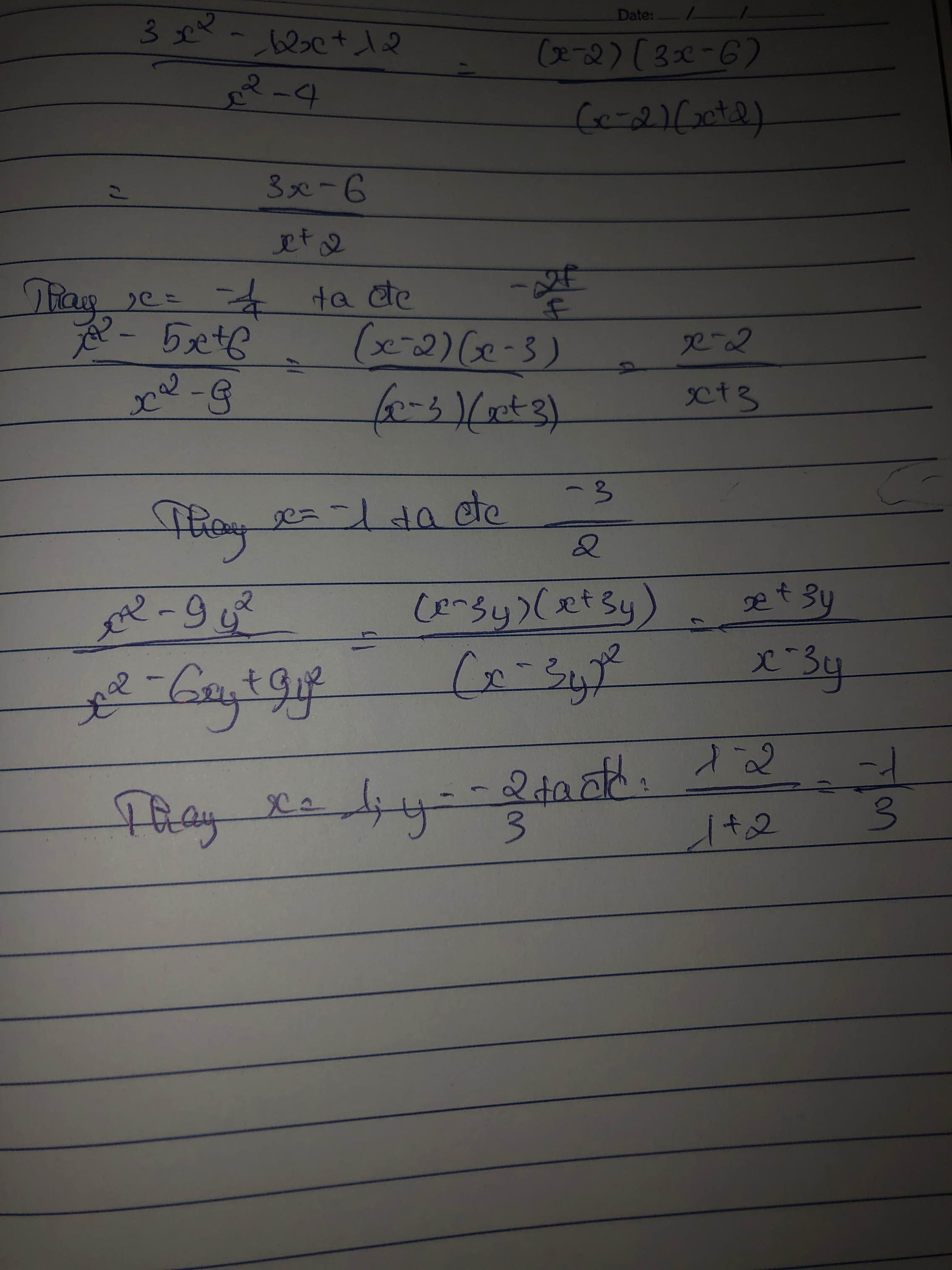

sory doan cuoi minh lam sai minh lam lai nhe
pt<=>1/(y-1)(y-2) + 1/(y-2)(y-3) + 1/(y-3)(y-4) + 1(y-4)(y-5)=1/15
=>1/(y-1) -1/(y-2)+1/(y-2)-1/(y-3)+1/(y-3)-1/(y-4)+1/(y-4)-1/(y-5)=1/15
=>1/(y-1) - 1/(y-5)=1/15
=>4/(y-1)(y-5)=1/15
=> (y-1)(y-5)=60
=> y2-6y+5-60=0
=>y2-6y-55=0
=> (y-11)(y+5)=0
=>y=11 hoac y=-5
pt<=> 1/(y-1)(y-2) + 1/(y-2)(y-3) + 1/(y-3)(y-4) + 1/(y-4)(y-5)=1/15
=>1/(y-1)-1/(y-2)+1/(y-2)-1/(y-3)+1/(y-3)-1/(y-4)+1/(y-4)-1/(y-5)=1/15
=>1/(y-1)-1/(y-5)=1/15
=>(y-1)(y-5)=-4.15=-60
=>y2-6y+65=0 k tim dc nghiem