K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
giải hộ mình vs ạ mình cần gấp ạ
YN
2
22 tháng 9 2021
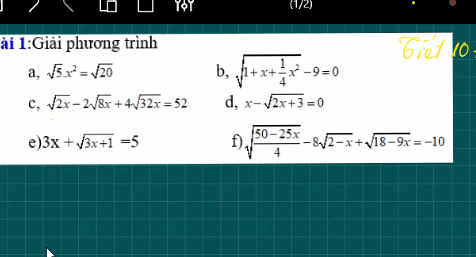
a) \(\Leftrightarrow x^2=\sqrt{4}\)
\(\Leftrightarrow x^2=2\Leftrightarrow x=\pm2\)
b) \(\Leftrightarrow\sqrt{\left(\dfrac{1}{2}x+1\right)^2}=9\)
\(\Leftrightarrow\left|\dfrac{1}{2}x+1\right|=9\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}x+1=9\\\dfrac{1}{2}x+1=-9\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=16\\x=-16\end{matrix}\right.\)
c) \(\Leftrightarrow\sqrt{2x}-4\sqrt{2x}+16\sqrt{2x}=52\left(đk:x\ge0\right)\)
\(\Leftrightarrow13\sqrt{2x}=52\Leftrightarrow\sqrt{2x}=4\Leftrightarrow2x=16\Leftrightarrow x=8\left(tm\right)\)
22 tháng 9 2021
f: Ta có: \(\sqrt{\dfrac{50-25x}{4}}-8\sqrt{2-x}+\sqrt{18-9x}=-10\)
\(\Leftrightarrow\sqrt{2-x}\cdot\dfrac{5}{2}-8\sqrt{2-x}+3\sqrt{2-x}=-10\)
\(\Leftrightarrow\sqrt{2-x}=4\)
\(\Leftrightarrow2-x=16\)
hay x=-14
PM
1
27 tháng 8 2021
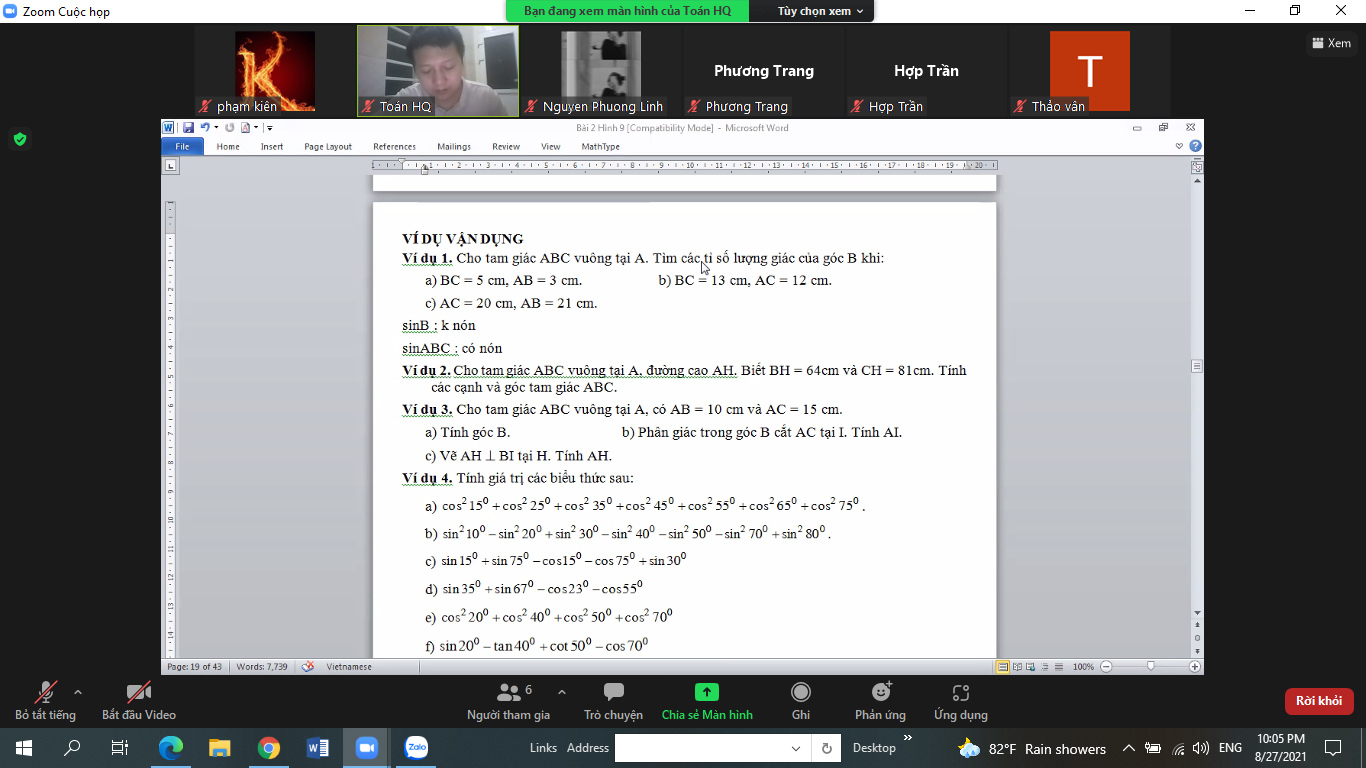
a: Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=10^2+15^2=325\)
hay \(BC=5\sqrt{13}\left(cm\right)\)
Xét ΔBAC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{15}{5\sqrt{13}}=\dfrac{3}{\sqrt{13}}\)
\(\Leftrightarrow\widehat{B}\simeq56^0\)
b: Xét ΔBAC có
BI là đường phân giác ứng với cạnh AC
nên \(\dfrac{AI}{AB}=\dfrac{CI}{BC}\)
hay \(\dfrac{AI}{10}=\dfrac{CI}{5\sqrt{13}}\)
mà AI+CI=15cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AI}{10}=\dfrac{CI}{5\sqrt{13}}=\dfrac{AI+CI}{10+5\sqrt{13}}=\dfrac{15}{10+5\sqrt{13}}=\dfrac{-2+\sqrt{13}}{3}\)
Do đó: \(AI=\dfrac{-20+10\sqrt{13}}{3}\left(cm\right)\)
KA
1
21 tháng 10 2021
Bài 3:
1: Ta có: \(P=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}-\dfrac{5\sqrt{x}+2}{x-4}\)
\(=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+2}\)
18 tháng 2 2021
1) Vì x=25 thỏa mãn ĐKXĐ nên Thay x=25 vào biểu thức \(A=\dfrac{\sqrt{x}-2}{x+1}\), ta được:
\(A=\dfrac{\sqrt{25}-2}{25+1}=\dfrac{5-2}{25+1}=\dfrac{3}{26}\)
Vậy: Khi x=25 thì \(A=\dfrac{3}{26}\)
2) Ta có: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}+\dfrac{2x+8\sqrt{x}-6}{x-\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-5\sqrt{x}+6+2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x+3\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-2}\)
VQ
0
26 tháng 9 2021
Bài 3:
a: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)
b: Thay x=9 vào A, ta được:
\(A=\dfrac{3-1}{3+1}=\dfrac{2}{4}=\dfrac{1}{2}\)
c: Ta có: P=AB
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\left(\dfrac{\sqrt{x}+3}{\sqrt{x}+1}+\dfrac{4}{\sqrt{x}-1}+\dfrac{5-x}{x-1}\right)\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\cdot\dfrac{x+2\sqrt{x}-3+4\sqrt{x}+4+5-x}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{6\sqrt{x}+6}{\left(\sqrt{x}+1\right)^2}=\dfrac{6}{\sqrt{x}+1}\)
:v chữ...