Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
e: \(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{1}{y}=1\\\dfrac{3}{x}+\dfrac{4}{y}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{x}-\dfrac{3}{y}=3\\\dfrac{3}{x}+\dfrac{4}{y}=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-7}{y}=-2\\\dfrac{1}{x}-\dfrac{1}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{7}{2}\\\dfrac{1}{x}=1+\dfrac{2}{7}=\dfrac{9}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{7}{2}\\x=\dfrac{7}{9}\end{matrix}\right.\)
Bài toán này có hai cách giải:
Cách 1: Thu gọn từng phương trình ta sẽ thu được phương trình bậc nhất hai ẩn x và y.
Cách 2: Đặt ẩn phụ.
Cách 1:
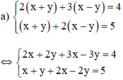
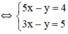(hệ số của y bằng nhau nên ta trừ từng vế hai phương trình)
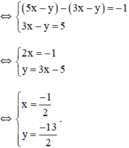
Vậy hệ phương trình có nghiệm duy nhất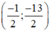 
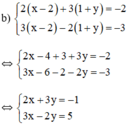
(Nhân hai vế pt 1 với 2; pt 2 với 3 để hệ số của y đối nhau)
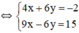(Hệ số của y đối nhau nên ta cộng từng vế của hai pt)
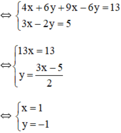
Vậy hệ phương trình có nghiệm duy nhất (1; -1).
Cách 2:
a) Đặt x + y = u và x – y = v (*)
Khi đó hệ phương trình trở thành
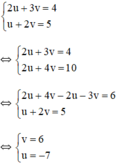
Thay u = -7 và v = 6 vào (*) ta được hệ phương trình:
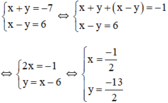
Vậy hệ phương trình có nghiệm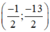 
b) Đặt x – 2 = u và y + 1 = v.
Khi đó hệ phương trình trở thành :
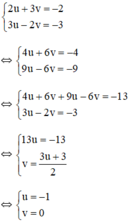
+ u = -1 ⇒ x – 2 = -1 ⇒ x = 1.
+ v = 0 ⇒ y + 1 = 0 ⇒ y = -1.
Vậy hệ phương trình có nghiệm (1; -1).
c) \(\left\{{}\begin{matrix}2\left(x-2\right)+3\left(1+y\right)=2\\3\left(x-2\right)-2\left(1+y\right)=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6\left(x-2\right)+9\left(1+y\right)=6\\6\left(x-2\right)-4\left(1+y\right)=-6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}13\left(1+y\right)=12\\2\left(x-2\right)+3\left(1+y\right)=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{21}{13}\\y=-\dfrac{1}{13}\end{matrix}\right.\)
d) \(\left\{{}\begin{matrix}\left(x-5\right)\left(y-2\right)=\left(x+2\right)\left(y-1\right)\\\left(x-4\right)\left(y+7\right)=\left(x-3\right)\left(y+4\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy-2x-5y+10=xy-x+2y-2\\xy+7x-4y-28=xy+4x-3y-12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x-7y=-12\\3x-y=16\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-x-7y=-12\\21x-7y=112\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}22x=124\\3x-y=16\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{62}{11}\\y=\dfrac{10}{11}\end{matrix}\right.\)
Ta có hệ : \(\hept{\begin{cases}x^2+y^2=\frac{1}{2}\\\left(x+y\right)^3+\left(x-y\right)^3=1\end{cases}}\) \(\Leftrightarrow\hept{\begin{cases}2x^2+2y^2=1\\2x^3+6xy^2=1\end{cases}\Leftrightarrow}\hept{\begin{cases}2y^2=1-2x^2\left(1\right)\\2x^3+6xy^2=1\left(2\right)\end{cases}}\)
Dễ thấy \(y=0\) không là nghiệm nên thế (1) và (2) ta có : \(2x^3+3.x.\left(1-2x^2\right)=1\)
\(\Leftrightarrow4x^3-3x+1=0\)
\(\Leftrightarrow\left(x+1\right)\left(2x-1\right)^2=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=-1\\x=\frac{1}{2}\end{cases}}\)
+) Với \(x=-1\) thì ta có : \(\hept{\begin{cases}\left(-1\right)^2+y^2=\frac{1}{2}\\\left(-1+y\right)^3+\left(-1-y\right)^3=1\end{cases}}\) ( Vô nghiệm )
+) Với \(x=\frac{1}{2}\) thì ta có : \(\left(\frac{1}{2}\right)^2+y^2=\frac{1}{2}\Leftrightarrow y=\pm\frac{1}{2}\). Thỏa mãn hệ phương trình.
Vậy hệ pt có 2 nghiệm \(\left(x,y\right)=\left\{\left(\frac{1}{2};-\frac{1}{2}\right),\left(\frac{1}{2},\frac{1}{2}\right)\right\}\)
a: \(\left\{{}\begin{matrix}x+4y=-11\\5x-4y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x=-10\\x+4y=-11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-5}{3}\\y=\dfrac{-11-x}{4}=\dfrac{-11+\dfrac{5}{3}}{4}=-\dfrac{7}{3}\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}2x-y=7\\3x+5y=-22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x-3y=21\\6x+15y=-66\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-18y=78\\2x-y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-13}{3}\\x=\dfrac{y+7}{2}=\dfrac{4}{3}\end{matrix}\right.\)
4:
x+3y=4m+4 và 2x+y=3m+3
=>2x+6y=8m+8 và 2x+y=3m+3
=>5y=5m+5 và x+3y=4m+4
=>y=m+1 và x=4m+4-3m-3=m+1
x+y=4
=>m+1+m+1=4
=>2m+2=4
=>2m=2
=>m=1
3:
x+2y=3m+2 và 2x+y=3m+2
=>2x+4y=6m+4 và 2x+y=3m+2
=>3y=3m+2 và x+2y=3m+2
=>y=m+2/3 và x=3m+2-2m-4/3=m+2/3
\(\left(x^3-y^3\right)-\left(x^2-y^2\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x^2+xy+y^2\right)-\left(x-y\right)\left(x+y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x^2+xy+y^2-x-y\right)=0\)
Làm nốt
\(a.\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{1}{y}-2=-1\\\dfrac{4}{x}+\dfrac{3}{y}-2=5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a-b-2=-1\\4a+3b-2=5\end{matrix}\right.\) (với \(\dfrac{1}{x}=a-\dfrac{1}{y}=b\))
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{10}{7}\\b=\dfrac{3}{7}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{10}{7}\Rightarrow x=\dfrac{7}{10}\\\dfrac{1}{y}=\dfrac{3}{7}\Rightarrow y=\dfrac{7}{3}\end{matrix}\right.\)
\(b.\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{5}{\left(x+y\right)}=2\\\dfrac{3}{x}+\dfrac{1}{\left(x+y\right)}=\dfrac{17}{10}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}2a+5b=2\\3a+b=\dfrac{17}{10}\end{matrix}\right.\) (với \(\dfrac{1}{x}=a-\dfrac{1}{x+y}=b\))
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=\dfrac{1}{5}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{2}\Rightarrow x=2\\\dfrac{1}{x+y}=\dfrac{1}{5}\Rightarrow y=3\end{matrix}\right.\)
\(c.\left\{{}\begin{matrix}\dfrac{2}{x-1}+\dfrac{1}{y+1}=7\\\dfrac{5}{x-1}-\dfrac{2}{y+1}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a+b=7\\5a-2b=4\end{matrix}\right.\) (với \(\dfrac{1}{x-1}=a-\dfrac{1}{y+1}=b\))
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=3\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x-1}=2\Rightarrow x=\dfrac{3}{2}\\\dfrac{1}{y+1}=3\Rightarrow y=-\dfrac{2}{3}\end{matrix}\right.\)
\(d.\left\{{}\begin{matrix}\dfrac{2}{\sqrt{x-1}}-\dfrac{1}{\sqrt{y-1}}=1\\\dfrac{1}{\sqrt{x-1}}+\dfrac{1}{\sqrt{y-1}}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a-b=1\\a+b=2\end{matrix}\right.\) (với \(\dfrac{1}{\sqrt{x-1}}=a-\dfrac{1}{\sqrt{y-1}}=b\))
\(\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{\sqrt{x-1}}=1\Rightarrow x=2\\\dfrac{1}{\sqrt{y-1}}=1\Rightarrow y=2\end{matrix}\right.\)
ĐKXĐ : \(xy\ne0\)
- Đặt \(x+\dfrac{1}{y}=t\)
\(\Rightarrow t^2=x^2+\dfrac{1}{y^2}+\dfrac{2x}{y}\)
\(\Rightarrow x^2+\dfrac{1}{y^2}=t^2-\dfrac{2x}{y}\)
Lại có từ PT ( II ) : \(\dfrac{x}{y}=3-\left(x+\dfrac{1}{y}\right)=3-t\)
\(\Rightarrow\dfrac{2x}{y}=6-2t\)
- Thay vào PT ( I ) ta được : \(t^2-\left(6-2t\right)+3-t=3\)
\(\Rightarrow t^2-6+2t+3-t-3=0\)
\(\Rightarrow t^2+t-6=0\)
\(\Rightarrow\left[{}\begin{matrix}t=2\\t=-3\end{matrix}\right.\)
TH1 : t = 2 .
=> \(x=y\)
Thay lại vào PT ( II ) ta được : \(x+\dfrac{1}{x}+1=3\)
\(\Rightarrow x^2+1-2x=0\)
\(\Rightarrow x=y=1\) ( TM )
TH2 : t = -3 .
=> \(x=6y\)
Thay lại vào PT ( II ) ta được : \(6y+\dfrac{1}{y}+6-3=0\)
\(\Rightarrow6y^2+1+3y=0\)
Vô nghiệm .
Vậy hệ phương trình có tập nghiệm \(S=\left\{\left(1;1\right)\right\}\)
1 x − x y = x 2 + x y − 2 y 2 ( 1 ) x + 3 − y 1 + x 2 + 3 x = 3 ( 2 )
Điều kiện: x > 0 y > 0 x + 3 ≥ 0 x 2 + 3 x ≥ 0 ⇔ x > 0 y > 0
( 1 ) ⇔ y − x y x = ( x − y ) ( x + 2 y ) ⇔ ( x − y ) x + 2 y + 1 y x = 0 ⇔ x = y do x + 2 y + 1 y x > 0 , ∀ x , y > 0
Thay y = x vào phương trình (2) ta được:
( x + 3 − x ) ( 1 + x 2 + 3 x ) = 3 ⇔ 1 + x 2 + 3 x = 3 x + 3 − x ⇔ 1 + x 2 + 3 x = x + 3 + x ⇔ x + 3 . x − x + 3 − x + 1 = 0 ⇔ ( x + 1 − 1 ) ( x − 1 ) = 0 ⇔ x + 3 = 1 x = 1 ⇔ x = − 2 ( L ) x = 1 ( t m ) ⇒ x = y = 1
Vậy hệ có nghiệm duy nhất (1;1)