K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DN
2
8 tháng 11 2021
Bài 4:
\(a,A=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\\ P=A:B=\dfrac{\sqrt{x}+1}{\sqrt{x}}\cdot\dfrac{x-1}{\sqrt{x}+1}=\dfrac{x-1}{\sqrt{x}}\\ b,P\sqrt{x}=m-\sqrt{x}+x\\ \Leftrightarrow x-1=m-\sqrt{x}+x\\ \Leftrightarrow m=\sqrt{x}-1\)
30 tháng 3 2023
9:
\(\text{Δ}=\left(-2m\right)^2-4\left(m^2-2m+4\right)\)
=4m^2-4m^2+8m-16=8m-16
Để phương trình có hai nghiệm phân biệt thì 8m-16>0
=>m>2
x1^2+x2^2=x1+x2+8
=>(x1+x2)^2-2x1x2-(x1+x2)=8
=>(2m)^2-2(m^2-2m+4)-2m=8
=>4m^2-2m^2+4m-8-2m=8
=>2m^2+2m-16=0
=>m^2+m-8=0
mà m>2
nên \(m=\dfrac{-1+\sqrt{33}}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 5 2021
\(Q=\dfrac{\sqrt{x}-3}{\sqrt{x}-1}=\dfrac{\sqrt{x}-1-2}{\sqrt{x}-1}=1-\dfrac{2}{\sqrt{x}-1}\)
\(\Rightarrow\sqrt{x}-1=Ư\left(2\right)=\left\{-2;-1;1;2\right\}\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}-1=-2\\\sqrt{x}-1=-1\\\sqrt{x}-1=1\\\sqrt{x}-1=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\sqrt{x}=-1\left(vn\right)\\\sqrt{x}=0\\\sqrt{x}=2\\\sqrt{x}=3\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=4\\x=9\end{matrix}\right.\)
U
1
8 tháng 6 2021
Nãy ghi nhầm =="
a)Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
Thay `m=1` vào pt ta có:
`x^2-2x-2-1=0`
`<=>x^2-2x-3=0`
`a-b+c=0`
`=>x_1=-1,x_2=3`
`=>y_1=1,y_2=9`
`=>(-1,1),(3,9)`
Vậy tọa độ gđ (d) và (P) là `(-1,1)` và `(3,9)`
b)
Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
PT có 2 nghiệm pb
`<=>Delta'>0`
`<=>1+2m+1>0`
`<=>2m> -2`
`<=>m> 01`
Áp dụng hệ thức vi-ét:`x_1+x_2=2,x_1.x_2=-2m-1`
Theo `(P):y=x^2=>y_1=x_1^2,y_2=x_2^2`
`=>x_1^2+x_2^2=14`
`<=>(x_1+x_2)^2-2x_1.x_2=14`
`<=>4-2(-2m-1)=14`
`<=>4+2(2m+1)=14`
`<=>2(2m+1)=10`
`<=>2m+1=5`
`<=>2m=4`
`<=>m=2(tm)`
Vậy `m=2` thì ....
25 tháng 6 2021
7)Đk \(x\le2\)
Pt \(\Leftrightarrow x^2-x+8=4-2x\)
\(\Leftrightarrow x^2+x+4=0\)
\(\Delta=-15< 0\) => vô nghiệm
Vậy pt vô nghiệm
10) \(\sqrt{9x+9}-4\sqrt{\dfrac{x+1}{4}}=5\) (đk: \(x\ge-1\)
\(\Leftrightarrow\sqrt{\left(x+1\right).9}-\dfrac{4\sqrt{x+1}}{\sqrt{4}}=5\)
\(\Leftrightarrow3\sqrt{x+1}-2\sqrt{x+1}=5\)
\(\Leftrightarrow\sqrt{x+1}=5\) \(\Leftrightarrow x=24\) (tm)
Vậy \(S=\left\{24\right\}\)
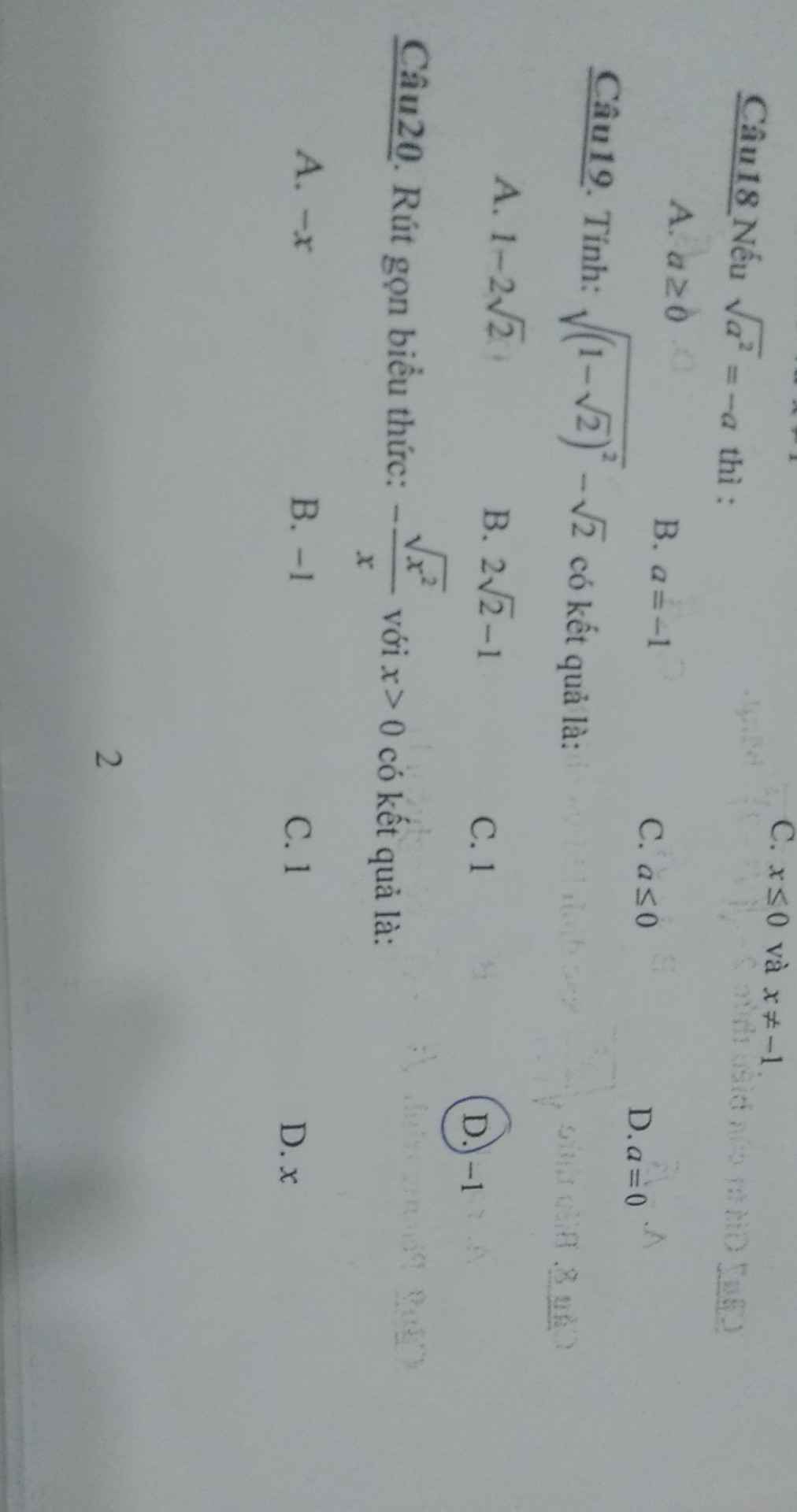
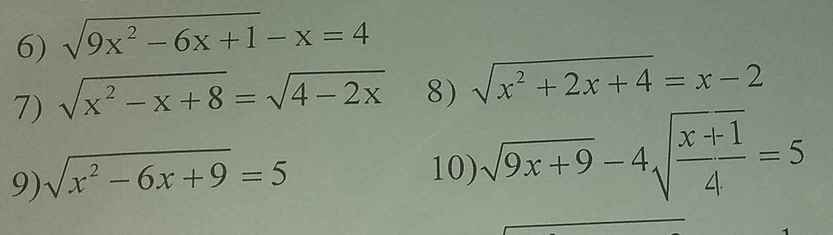
Câu 17: C
Câu 18: C