Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

4.
\(\lim\limits_{x\rightarrow8}f\left(x\right)=\lim\limits_{x\rightarrow8}\dfrac{\sqrt[3]{x}-2}{x-8}=\lim\limits_{x\rightarrow8}\dfrac{x-8}{\left(x-8\right)\left(\sqrt[3]{x^2}+2\sqrt[3]{x}+4\right)}=\lim\limits_{x\rightarrow8}\dfrac{1}{\sqrt[3]{x^2}+2\sqrt[3]{x}+4}\)
\(=\dfrac{1}{4+4+4}=\dfrac{1}{12}\)
\(f\left(8\right)=3.8-20=4\)
\(\Rightarrow\lim\limits_{x\rightarrow8}f\left(x\right)\ne f\left(8\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=8\)
5.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{1+2x}-1+1-\sqrt[3]{1+3x}}{x}=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{2x}{\sqrt[]{1+2x}+1}-\dfrac{3x}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}}{x}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{2}{\sqrt[]{1+2x}+1}-\dfrac{3}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}\right)=\dfrac{2}{1+1}-\dfrac{3}{1+1+1}=0\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(3x^2-2x\right)=0\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=f\left(0\right)\)
\(\Rightarrow\) Hàm liên tục tại \(x=0\)
6.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\sqrt[3]{6x+1}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\left(2x+1\right)+\left(2x+1-\sqrt[3]{6x+1}\right)}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{-x^2}{\sqrt[]{4x+1}+2x+1}+\dfrac{x^2\left(8x+12\right)}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{-1}{\sqrt[]{4x+1}+2x+1}+\dfrac{8x+12}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}\right)\)
\(=\dfrac{-1}{1+1}+\dfrac{12}{1+1+1}=\dfrac{7}{2}\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(2-3x\right)=2\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)\ne\lim\limits_{x\rightarrow0^-}f\left(x\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=0\)


`y'=[3(x+1)-3x-2]/[(x+1)^2]=1/[(x+1)^2]`
Gọi `M(x_0; y_0)-` tiếp điểm
Mà `y_0=[3x_0+2]/[x_0+1] in T T`
`=>y-[3x_0+2]/[x_0+1]=1/[(x_0+1)^2](x-x_0)`
`@` Gọi `T T nn Ox =A`
`=>-[3x_0+2]/[x_0+1]=1/[(x_0+1)^2](x-x_0)`
`<=>(-3x_0 -2)(x_0+1)=x-x_0`
`<=>-3x_0 ^2-3x_0 -2x_0 -2=x-x_0`
`<=>x=-3x_0 ^2-4x_0 -2`
`=>OA=|-3x_0 ^2-4x_0 -2|`
`@` Gọi `T T nn Oy=B`
`=>y-[3x_0 +2]/[x_0 +1]=1/[(x_0 +1)^2](-x_0)`
`<=>y=[(3x_0+2)(x_0+1)-x_0]/[(x_0+1)^2]`
`<=>y=[3x_0 ^2+4x_0 +2]/[(x_0 +1)^2]`
`=>OB=|[3x_0 ^2+4x_0 +2]/[(x_0 +1)^2]|`
Vì `\triangle OAB` vuông cân tại `O`
`=>OA=OB`
`<=>|-3x_0 ^2-4x_0 -2|=|[3x_0 ^2+4x_0 +2]/[(x_0 +1)^2]|`
`<=>(x_0+1)^2=1`
`<=>[(x_0=0),(x_0=-2):}`
`=>` PTTT: `[(y=x+2),(y=x+6):}`

1.
\(-1\le sin\left(x-\dfrac{\pi}{2}\right)\le1\Rightarrow1\le y\le5\)
\(y_{min}=1\) khi \(sin\left(x-\dfrac{\pi}{2}\right)=-1\)
\(y_{max}=5\) khi \(sin\left(x-\dfrac{\pi}{2}\right)=1\)
2.
\(-1\le cos2x\le1\Rightarrow\dfrac{5}{2}\le y\le\dfrac{7}{2}\)
\(y_{min}=\dfrac{5}{2}\) khi \(cos2x=1\)
\(y_{max}=\dfrac{7}{2}\) khi \(cos2x=-1\)
3.
\(0\le cos^2\left(2x+\dfrac{\pi}{3}\right)\le1\Rightarrow-2\le y\le-1\)
\(y_{min}=-2\) khi \(cos\left(2x+\dfrac{\pi}{3}\right)=\pm1\)
\(y_{max}=-1\) khi \(cos\left(2x+\dfrac{\pi}{3}\right)=0\)
4.
\(-1\le cos\left(4x^2\right)\le1\Rightarrow-2\le y\le\sqrt{2}-2\)
\(y_{min}=-1\) khi \(cos\left(4x^2\right)=-1\)
\(y_{max}=\sqrt{2}-2\) khi \(cos\left(4x^2\right)=1\)

TXĐ: `D=RR\\{π/2+kπ ; -π/4 +kπ}`
Mà `-π/2+k2π` và `π/2+k2π \in π/2 +kπ`
`=>` Không nằm trong TXĐ.

Vậy hãy sử dụng 1 phương pháp giải khác tối ưu hơn:
\(\Leftrightarrow2sin^22x=1\)
\(\Leftrightarrow1-2sin^22x=0\)
\(\Leftrightarrow cos4x=0\)
\(\Leftrightarrow4x=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\)
Với cách giải này thì nghiệm được gộp luôn

Gọi abc là stn có ba chữ số khác nhau cần tìm
TH1: c = {0} -> 1cc TH2: c = {2;4;6} -> 3cc
a \ {c} -> 6cc a \ {0;c) -> 5cc
b \ {a;c} -> 5cc b \ {a;c} -> 5cc
<=>(6*5)+(3*5*5)=105 số
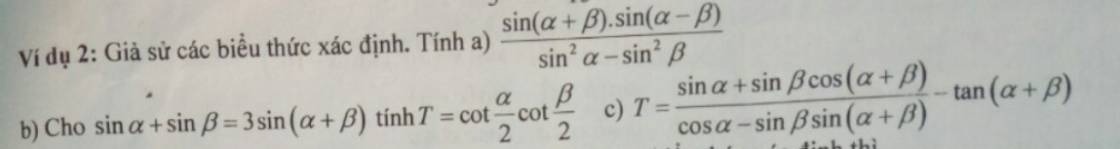



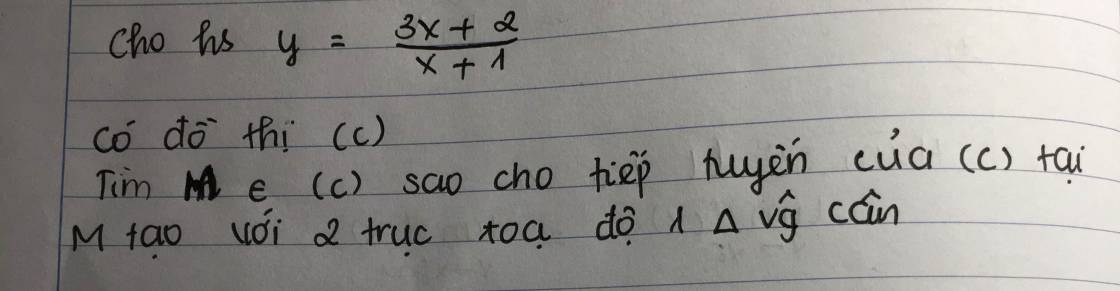

a: \(=\dfrac{-\dfrac{1}{2}\left[cos\left(a+b+a-b\right)-cos\left(a+b-a+b\right)\right]}{cos^2b-cos^2a}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left[cos2a-cos2b\right]}{\dfrac{1-cos2b}{2}-\dfrac{1-cos2a}{2}}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1-cos2b-1+cos2a}{2}}=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}=-1\)
c: \(T=\dfrac{sina+sinb\cdot\left(cosa\cdot cosb-sina\cdot sinb\right)}{cosa-sinb\cdot\left(sina\cdot cosb+sinb\cdot cosa\right)}-tan\left(a+b\right)\)
\(=\dfrac{sina+sinb\cdot cosa\cdot cosb-sin^2b\cdot sina}{cosa-sinb\cdot sina\cdot cosb-sin^2b\cdot cosa}-tan\left(a+b\right)\)
\(=\dfrac{sina\left(1-sin^2b\right)+sinb\cdot cosa\cdot cosb}{cosa\left(1-sin^2b\right)-sinb\cdot sina\cdot cosb}\)-tan(a+b)
\(=\dfrac{sina\cdot cos^2b+sinb\cdot cosa\cdot cosb}{cosa\cdot cos^2b-sinb\cdot sina\cdot cosb}-tan\left(a+b\right)\)
\(=\dfrac{sina\cdot cosb+sinb\cdot cosa}{cosa\cdot cosb-sina\cdot sinb}-tan\left(a+b\right)\)
\(=\dfrac{sin\left(a+b\right)}{cos\left(a+b\right)}-tan\left(a+b\right)=0\)