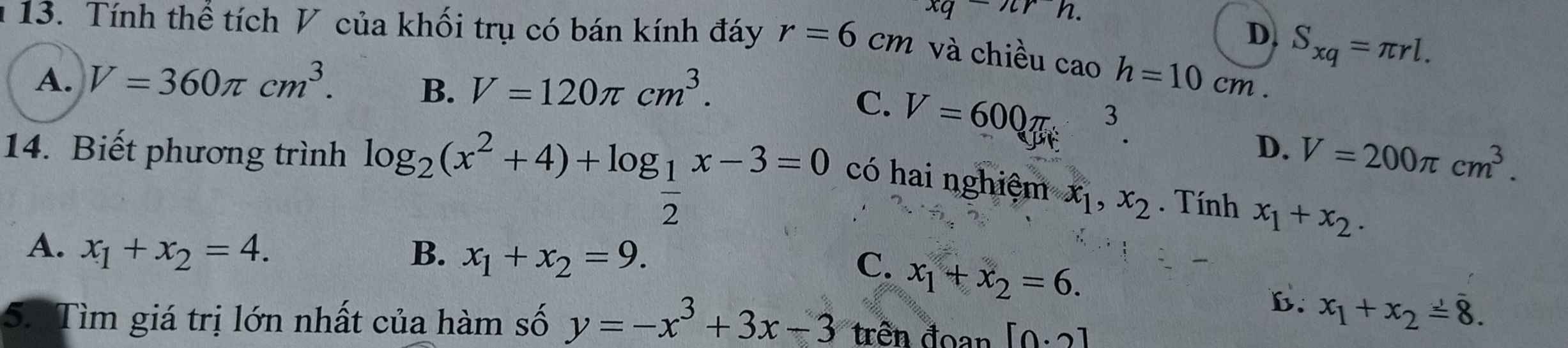giải giúp e câu 2,4,5,6 vs ạ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2022
ĐKXĐ: \(x>0\)
\(log_2\left(x^2+4\right)-log_2x-3=0\)
\(\Leftrightarrow log_2\left(x^2+4\right)=log_2x+3\)
\(\Leftrightarrow log_2\left(x^2+4\right)=log_2\left(9x\right)\)
\(\Leftrightarrow x^2+4=9x\)
\(\Leftrightarrow x^2-9x+4=0\)
\(\Rightarrow x_1+x_2=9\) theo định lý Viet
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 3 2021
11. \(I=\int\limits^2_1x\sqrt{x^2+1}dx\)
Đặt \(\sqrt{x^2+1}=t\Leftrightarrow x^2=t^2-1\Rightarrow xdx=tdt\) ; \(\left\{{}\begin{matrix}x=1\Rightarrow t=\sqrt{2}\\x=2\Rightarrow t=\sqrt{5}\end{matrix}\right.\)
\(I=\int\limits^{\sqrt{5}}_{\sqrt{2}}t.tdt=\int\limits^{\sqrt{5}}_{\sqrt{2}}t^2dt=\dfrac{1}{3}t^3|^{\sqrt{5}}_{\sqrt{2}}=\dfrac{1}{3}\left(5\sqrt{5}-2\sqrt{2}\right)\)
12. Đặt \(\sqrt[3]{8-4x}=t\Rightarrow x=\dfrac{8-t^3}{4}\Rightarrow dx=-\dfrac{3}{4}t^2dt\) ; \(\left\{{}\begin{matrix}x=0\Rightarrow t=2\\x=2\Rightarrow t=0\end{matrix}\right.\)
\(I=\int\limits^0_2t.\left(-\dfrac{3}{4}t^2dt\right)=\dfrac{3}{4}\int\limits^2_0t^3dt=\dfrac{3}{16}t^4|^2_0=3\)
13. Đặt \(\sqrt{3-2x}=t\Rightarrow x=\dfrac{3-t^2}{2}\Rightarrow dx=-tdt\) ; \(\left\{{}\begin{matrix}x=0\Rightarrow t=\sqrt{3}\\x=1\Rightarrow t=1\end{matrix}\right.\)
\(I=\int\limits^1_{\sqrt{3}}\dfrac{-tdt}{t}=\int\limits^{\sqrt{3}}_1dt=t|^{\sqrt{3}}_1=\sqrt{3}-1\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 6 2021
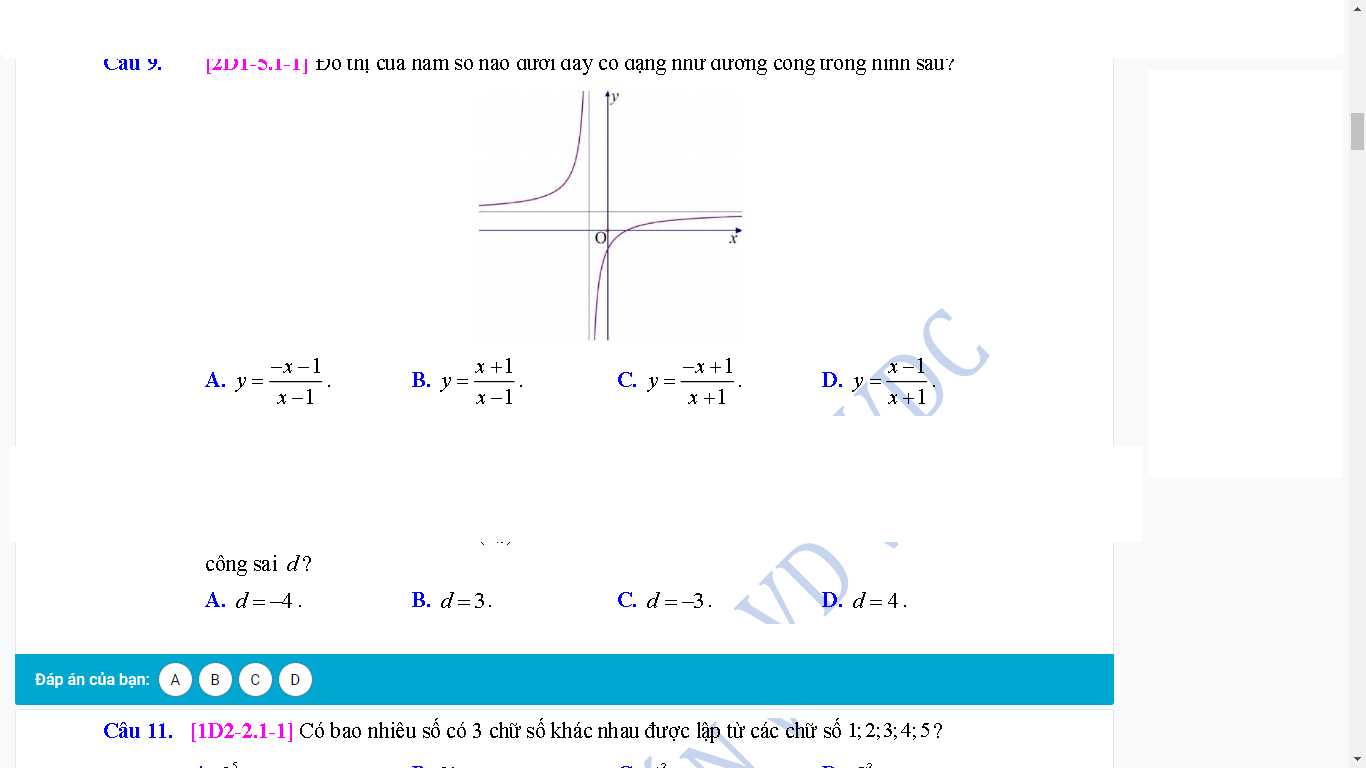
- Tiệm cận đứng của đồ thị là 1 giá trị âm nên loại A và B
- Hàm đồng biến trên các khoảng xác định nên loại C
Vậy D là đáp án đúng
LT
0
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2022
Đồ thị hàm số cắt trục hoành tại 3 điểm pb \(\Leftrightarrow x^3-3x^2+m+1=0\) có 3 nghiệm pb
\(\Leftrightarrow-x^3+3x^2-1=m\) có 3 nghiệm pb
Xét hàm \(f\left(x\right)=-x^3+3x^2-1=0\)
\(f'\left(x\right)=-3x^2+6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
\(f\left(0\right)=-1\) ; \(f\left(2\right)=3\)
\(\Rightarrow\) Pt có 3 nghiệm pb khi \(-1< m< 3\)