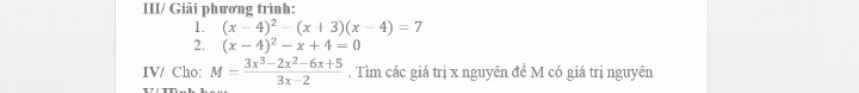K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 12 2021
\(a,\Delta ABC\text{ cân }A\Rightarrow AH\text{ cũng là trung tuyến}\\ \left\{{}\begin{matrix}BH=HC\\AH=HE\end{matrix}\right.\Rightarrow ABEC\text{ là hbh}\\ \text{Mà }AE\bot BC=\left\{H\right\}\Rightarrow ABEC\text{ là hình thoi}\\ b,\text{Vì }D,F\text{ là trung điểm }AH,HC\Rightarrow DF\text{ là đtb }\Delta AHC\\ \Rightarrow DF=\dfrac{1}{2}AC\\ \text{Xét }\Delta AHC\bot H\Rightarrow HI=\dfrac{1}{2}AC\left(\text{trung tuyến ứng cạnh huyền }\right)\\ \Rightarrow DF=HI\)
19 tháng 12 2021
a: Xét tứ giác ABEC có
H là trung điểm của AE
H là trung điểm của BC
Do đó: ABEC là hình bình hành
mà AB=AC
nên ABEC là hình thoi
LT
1
NH
0
9 tháng 3 2022
a, Xét tứ giác ADHE có ^ADH = ^AEH = ^DAE = 900
=> tứ giác ADHE là hcn
=> AH = DE (2 đường chéo bằng nhau)
b, Xét tam giác AHB và tam giác CHA ta có
^AHB = ^CHA = 900
^HAB = ^HCA ( cùng phụ ^HAC )
Vậy tam giác AHB~ tam giác CHA (g.g)
\(\dfrac{AH}{CH}=\dfrac{HB}{AH}\Rightarrow AH^2=BH.CH\)
c, Xét tam giác AHD và tam giác ABH có
^ADH = ^AHB = 900
^A _ chung
Vậy tam giác AHD ~ tam giác ABH (g.g)
\(\dfrac{AH}{AB}=\dfrac{AD}{AH}\Rightarrow AH^2=AD.AB\)(1)
tương tự tam giác AEH ~ tam giác AHC (g.g)
\(\dfrac{AE}{AH}=\dfrac{AH}{AC}\Rightarrow AH^2=AE.AC\left(2\right)\)
Từ (1) ; (2) suy ra \(AD.AB=AE.AC\Rightarrow\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Xét tam giác ADE và tam giác ACB
^A _ chung
\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\left(cmt\right)\)
Vậy tam giác ADE ~ tam giác ACB (c.g.c)
22 tháng 10 2021
\(5x^2+10xy-4x-8y\)
\(=5x\left(x+2y\right)-4\left(x+2y\right)\)
\(=\left(x+2y\right)\left(5x-4\right)\)
AH
Akai Haruma
Giáo viên
30 tháng 10 2021
Lời giải:
a.
$=(5x^2+5xy)+(10x+10y)=5x(x+y)+10(x+y)$
$=(x+y)(5x+10)=5(x+y)(x+2)$
b. Biểu thức không phân tích được thành nhân tử.
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
4 tháng 7 2023
a/
\(\widehat{BAE}+\widehat{DAE}=\widehat{BAD}=90^o\)
\(\widehat{DAF}+\widehat{DAE}=\widehat{FAE}=90^o\)
\(\Rightarrow\widehat{BAE}=\widehat{DAF}\) (cùng phụ với \(\widehat{DAE}\) ) (1)
\(AB=AD\) (cạnh hình vuông) (2)
Xét tg vuông ABE và tg vuông ADF
Từ (1) và (2) => tg ABE = tg ADF (Hai tg vuông có cạnh góc vuông và góc nhọn tương ứng bằng nhau)
\(\Rightarrow AE=AF\) (đpcm)
b/
AE=AF (cmt) => tg AEF là tg cân tại A
I là trung điểm EF (gt)
=> AI là trung tuyến thuộc EF => \(AI\perp EF\) (tring tg cân đường trung tuyến xp từ đỉnh tg cân đồng thời là đường cao)
\(\Rightarrow GK\perp EF\) (3)
Xét tg EIG và tg FIK có
\(\widehat{EIG}=\widehat{FIK}\) (góc đối đỉnh) (4)
EG//AB; AB//CD => EG//CD => EG//FK (5)
\(\Rightarrow\widehat{GEI}=\widehat{KFI}\) (góc so le trong) (6)
\(IE=IF\) (gt) (7)
Từ (4) (6) (7) => tg EIG = tg FIK (g.c.g) => EG = FK (8)
Từ (5) và (8) => EGFK là hình bình hành (Tứ giác có cặp cạnh đối // và = nhau là hình bình hành) (9)
Từ (3) và (9) => EGFK là hình thoi (hình bình hành có hai đường chéo vuông góc với nhau là hình thoi) (đpcm)
c/
Ta có tg AEF cân tại A (cmt); AI là trung tuyến thuộc EF (cmt)
=> AI là phân giác \(\widehat{EAF}\) (trong tg cân đường trung tuyến xp từ đỉnh tg cân đồng thời là đường phân giác của góc ở đỉnh)
Mà \(\widehat{EAF}=90^o\)
\(\Rightarrow\widehat{FAK}=45^o\)
\(\widehat{ACF}=45^o\)
\(\Rightarrow\widehat{FAK}=\widehat{ACF}=45^o\)
Xét tg AKF và tg ACF có
\(\widehat{FAK}=\widehat{ACF}=45^o\)
\(\widehat{AFC}\) chung
=> tg AKF đồng dạng với tg CAF (g.g.g)
d/
17 tháng 11 2021
\(1,\Leftrightarrow x^2-8x+16-x^2+x+12=7\\ \Leftrightarrow-7x=-21\\ \Leftrightarrow x=3\\ 2,\Leftrightarrow\left(x-4\right)^2-\left(x-4\right)=0\\ \Leftrightarrow\left(x-4\right)\left(x-5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=4\\x=5\end{matrix}\right.\)