K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 9 2021
\(A=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\right)\left(1-\dfrac{1}{\sqrt{x}}\right)\left(đk:x>0,x\ne1\right)\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2-\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}-1}{\sqrt{x}}\)
\(=\dfrac{x+2\sqrt{x}+1-x+2\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\dfrac{4\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}=\dfrac{4}{\sqrt{x}+1}\)
AH
Akai Haruma
Giáo viên
26 tháng 6 2023
2.7
a/ $9+4\sqrt{5}=2^2+2.2\sqrt{5}+(\sqrt{5})^2=(2+\sqrt{5})^2$
b/ $\sqrt{9+4\sqrt{5}}-\sqrt{5}=\sqrt{(2+\sqrt{5})^2}-\sqrt{5}$
$=|2+\sqrt{5}|-\sqrt{5}=2+\sqrt{5}-\sqrt{5}=2$
c/ $\sqrt{23+8\sqrt{7}}-\sqrt{7}=\sqrt{4^2+2.4\sqrt{7}+(\sqrt{7})^2}-\sqrt{7}=\sqrt{(4+\sqrt{7})^2}-\sqrt{7}$
$=4+\sqrt{7}-\sqrt{7}=4$
d.
$\sqrt{a+4\sqrt{a-2}+2}+\sqrt{a-4\sqrt{a-2}+2}$
$=\sqrt{(a-2)+2.2\sqrt{a-2}+2^2}+\sqrt{(a-2)-2.2\sqrt{a-2}+2^2}$
$=\sqrt{(\sqrt{a-2}+2)^2}+\sqrt{(\sqrt{a-2}-2)^2}$
$=|\sqrt{a-2}+2|+|\sqrt{a-2}-2|$
$=\sqrt{a-2}+2+2-\sqrt{a-2}=4$ (do $a\leq 6$ nên $\sqrt{a-2}-2\leq 0$ nên $|\sqrt{a-2}-2|=2-\sqrt{a-2}$)
AH
Akai Haruma
Giáo viên
26 tháng 6 2023
2.5
a.
$\sqrt{(x-3)^2}=3-x$
$\Leftrightarrow |x-3|=3-x$
$\Leftrightarrow 3-x\geq 0$
$\Leftrightarrow x\leq 3$
b.
$\sqrt{25-20x+4x^2}+2x=5$
$\Leftrightarrow \sqrt{(2x-5)^2}=5-2x$
$\Leftrightarrow |2x-5|=5-2x$
$\Leftrightarrow 5-2x\geq 0$
$\Leftrightarrow x\leq \frac{2}{5}$
c.
$\sqrt{x^2-\frac{1}{2}x+\frac{1}{16}}=\frac{1}{4}-x$
$\Leftrightarrow \sqrt{(x-\frac{1}{4})^2}=\frac{1}{4}-x$
$\Leftrightarrow |x-\frac{1}{4}|=\frac{1}{4}-x$
$\Leftrightarrow \frac{1}{4}-x\geq 0$
$\Leftrightarrow x\leq \frac{1}{4}$
V
0
V
0
BT
7
13 tháng 7 2021
1) Ta có: \(\sqrt{2x+5}=\sqrt{3-x}\)
\(\Leftrightarrow2x+5=3-x\)
\(\Leftrightarrow2x+x=3-5\)
\(\Leftrightarrow3x=-2\)
hay \(x=-\dfrac{2}{3}\)
2) Ta có: \(\sqrt{2x-5}=\sqrt{x-1}\)
\(\Leftrightarrow2x-5=x-1\)
\(\Leftrightarrow2x-x=-1+5\)
\(\Leftrightarrow x=4\)
PN
23 tháng 8 2021
3 , \(PT\left(đk:\frac{16}{3}\ge x\ge3\right)< =>x^2-3x=16-3x\)
\(< =>x^2-16=0< =>\left(x-4\right)\left(x+4\right)=0< =>\orbr{\begin{cases}x=4\left(tm\right)\\x=-4\left(ktm\right)\end{cases}}\)
4 , \(PT\left(đk:...\right)< =>2x^2-3=4x-3< =>2x^2-4x=0\)
\(< =>2x\left(x-2\right)=0< =>\orbr{\begin{cases}x=0\left(...\right)\\x=2\left(...\right)\end{cases}}\)
bạn tự tìm đk rồi đối chiếu nhé :P
BT
5
13 tháng 7 2021
1) Ta có: \(\sqrt{4x}=\sqrt{5}\)
nên 4x=5
hay \(x=\dfrac{5}{4}\)
2) Ta có: \(\sqrt{16x}=8\)
nên 16x=64
hay x=4
PN
23 tháng 8 2021
3, \(2\sqrt{x}=\sqrt{9x}-3\left(đk:x\ge0\right)\)
\(< =>2\sqrt{x}-3\sqrt{x}+3=0\)
\(< =>3-\sqrt{x}=0< =>x=9\)(tmđk)
4, \(\sqrt{3x-1}=4\left(đk:x\ge\frac{1}{3}\right)\)
\(< =>3x-1=16< =>3x-17=0\)
\(< =>x=\frac{17}{3}\)(tmđk)
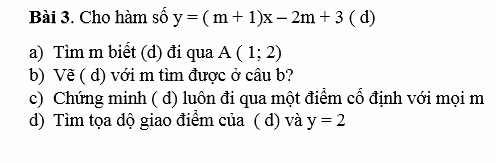
\(a,A=\left(1;2\right)\Leftrightarrow x=1;y=2\\ \Leftrightarrow2=\left(m+1\right)-2m+3\\ \Leftrightarrow-m+4=2\Leftrightarrow m=2\)
\(c,\)Giả sử điểm cố định là \(A\left(x_0;y_0\right)\)
\(\Leftrightarrow y_0=\left(m+1\right)x_0-2m+3\\ \Leftrightarrow y_0=mx_0+x_0-2m+3\\ \Leftrightarrow m\left(x_0-2\right)+\left(x_0-y_0+3\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0-2=0\\x_0-y_0+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=2\\y_0=5\end{matrix}\right.\Leftrightarrow B\left(2;5\right)\)
Vậy \(\left(d\right)\) luôn đi qua điểm \(B\left(2;5\right)\) cố định
\(d,\) Pt hoành độ giao điểm:
\(2=\left(2+1\right)x-2\cdot2+3\\ \Leftrightarrow2=3x-1\Leftrightarrow x=1\\ \Leftrightarrow C\left(1;2\right)\)
Vậy ...