
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(VP=a^3+b^3+c^3-3bac\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=VT\)
b: \(VT=\left(3a+2b-1\right)\left(a+5\right)-2b\left(a-2\right)\)
\(=3a^2+15a+2ab+10b-a-5-2ab+4b\)
\(=3a^2+14a+14b-5\)
\(VP=\left(3a+5\right)\left(a+3\right)+2\left(7b-10\right)\)
\(=3a^2+9a+5a+15+14b-20\)
\(=3a^2+14a+14b-5\)
=>VT=VP
c: \(VT=a\left(b-x\right)+x\left(a+b\right)\)
\(=ab-ax+ax+bx\)
\(=ab+bx=b\left(a+x\right)=VP\)
d: \(VT=a\left(b-c\right)-b\left(a+c\right)+c\left(a-b\right)\)
\(=ab-ac-ab-bc+ca-cb\)
\(=-2bc\)
=VP

a1/\(\dfrac{2}{x+y}+\dfrac{1}{x-y}+\dfrac{-3x}{x^2-y^2}\)
\(=\dfrac{2\left(x-y\right)}{\left(x+y\right)\left(x-y\right)}+\dfrac{x+y}{\left(x+y\right)\left(x-y\right)}+\dfrac{-3x}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{2x-2y+x+y-3x}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{-y}{\left(x+y\right)\left(x-y\right)}\)
a2/\(\dfrac{5x^2-y^2}{xy}-\dfrac{3x-2y}{y}\)
\(=\dfrac{5x^2-y^2}{xy}-\dfrac{3x^2-2xy}{xy}\)
\(=\dfrac{5x^2-y^2-3x^2+2xy}{xy}\)
\(=\dfrac{2x^2-y^2+2xy}{xy}\)
b/\(\dfrac{2x}{x^2+2xy}+\dfrac{y}{xy-2y^2}+\dfrac{4}{x^2-4y^2}\)
\(=\dfrac{2x}{x\left(x+2y\right)}+\dfrac{y}{y\left(x-2y\right)}+\dfrac{4}{\left(x-2y\right)\left(x+2y\right)}\)
\(=\dfrac{2}{x+2y}+\dfrac{1}{x-2y}+\dfrac{4}{\left(x-2y\right)\left(x+2y\right)}\)
\(=\dfrac{2\left(x-2y\right)}{\left(x-2y\right)\left(x+2y\right)}+\dfrac{x+2y}{\left(x-2y\right)\left(x+2y\right)}+\dfrac{4}{\left(x-2y\right)\left(x+2y\right)}\)
\(=\dfrac{2x-4y+x+2y+4}{\left(x-2y\right)\left(x+2y\right)}\)
\(=\dfrac{3x-2y+4}{\left(x-2y\right)\left(x+2y\right)}\)
#TienDatzZz
a) \(\dfrac{2}{x+y}+\dfrac{1}{x-y}+\dfrac{-3x}{x^2-Y^2}\)
\(\dfrac{2\left(x-y\right)}{\left(x+y\right)\left(x-y\right)}+\dfrac{\left(x+y\right)}{\left(x+y\right)\left(x-y\right)}+\dfrac{-3x}{x^2-y^2}\)
\(\dfrac{2x-2y+x+y-3x}{x^2-y^2}\)
\(\dfrac{-y}{x^2-y^2}\)

Lời giải:
Gọi giá của tivi ban đầu là $a$ đồng.
Giá tivi đầu tháng: $a(1+0,05)=1,05a$ (đồng)
Giá tivi của tháng: $1,05a(1-0,05)=0,9975a$ (đồng)
Chênh lệch giá ti vi ban đầu và cuối tháng là:
$a-0,9975a=50000$
$a.0,0025=50000$
$a=20000000$ (đồng)


Tham khaor
a) C/M DBEC là HBH
Ta có BE//CD (vì AB//CD)
BE=CD (cùng bằng AB)
Vậy DBEC là HBH
b) C/M E đxứng F qua C
Ta có BD//CE (vì DBEC là HBH)
Mà BD//EF (T/C đtb △AEF)
Nên E, C, F thẳng hàng (1)
Lại có BDFC là HBH (BC//DF và BC=DF)
⇒BD=CF
Mà BD=CE (vì DBEC là HBH)
Nên CE=CF (2)
Từ (1) và (2) suy ra, E đxứng F qua C

các câu sau khuyến khích bn tự làm
a,\(12x^2y-18xy^2-30y^3=6y\left(2x^2-3xy-5y^2\right)\)
b,\(16x^2\left(x-y\right)-10y\left(y-x\right)=16x^2\left(x-y\right)+10y\left(x-y\right)=\left(x-y\right)\left(16x^2+10y\right)=2\left(x-y\right)\left(8x^2+5y\right)\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ c,x^3+9x^2+27x+27=x^3+3.3.x^2+3.3^2.x+3^3=\left(x+3\right)^3\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ d.8x^3+36x^2y+54xy^2+27y^3=\left(2x\right)^3+3.2^2.3x^2y+3.2.3^2xy^2+\left(3y\right)^3=\left(2x+3y\right)^3\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ e,\left(x-y\right)^2-4=\left(x-y\right)^2-2^2=\left(x-y-2\right)\left(x+y+2\right)\\ \\ \\ \\ \\ g,16x^2-9\left(x+y\right)^2=\left(4x\right)^2-\left[3\left(x+y\right)\right]^2=\left(4x-3x-3y\right)\left(4x+3x+3y\right)=\left(x-3y\right)\left(7x+3y\right) \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ h.5x^2-5xy-10x+10y=\left(5x^2-10x\right)-\left(5xy-10y\right)=5x\left(x-2\right)-5y\left(x-2\right)=\left(x-y\right)5\left(x-2\right)\)

Bài 2:
a) Ta có: AB=AD(gt)
nên A nằm trên đường trung trực của BD(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: CB=CD(gt)
nên C nằm trên đường trung trực của BD(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AC là đường trung trực của BD(Đpcm)
b) Ta có: \(\widehat{BCD}=60^0\)
nên \(\widehat{CBD}=\widehat{CDB}=60^0\)
Ta có: \(\widehat{BAD}=100^0\)
nên \(\widehat{ABD}=\widehat{ADB}=\dfrac{180^0-100^0}{2}=\dfrac{80^0}{2}=40^0\)
\(\Leftrightarrow\widehat{ABC}=100^0;\widehat{ADC}=100^0\)


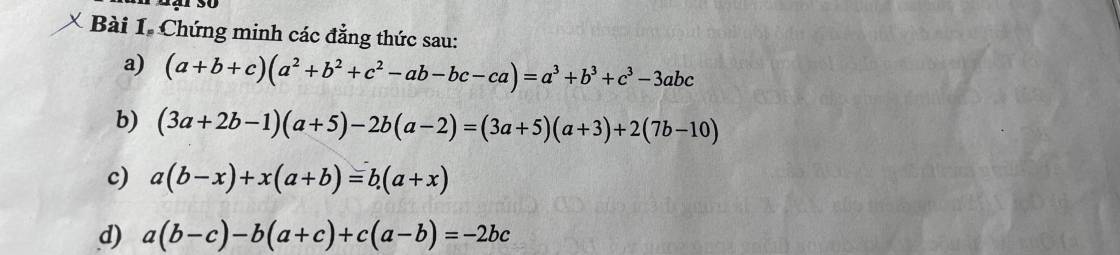
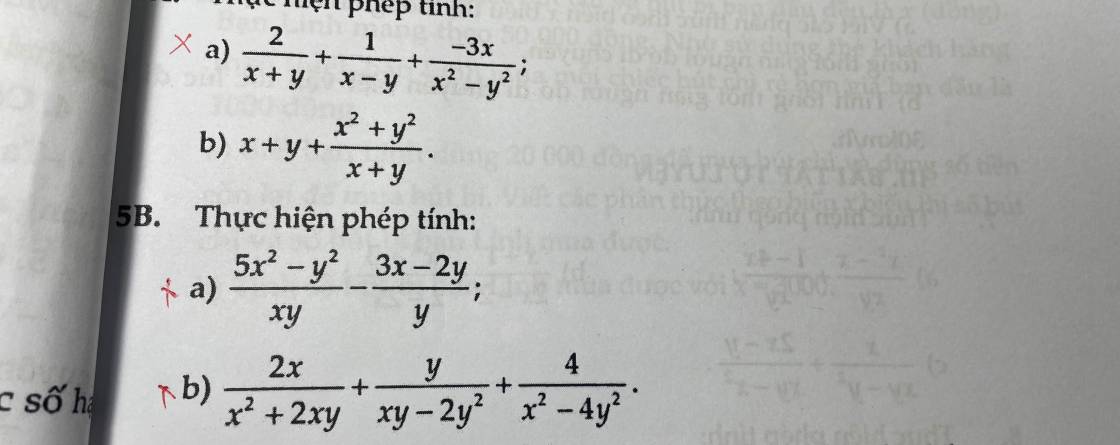
 Dag cần gấp giúp mk
Dag cần gấp giúp mk
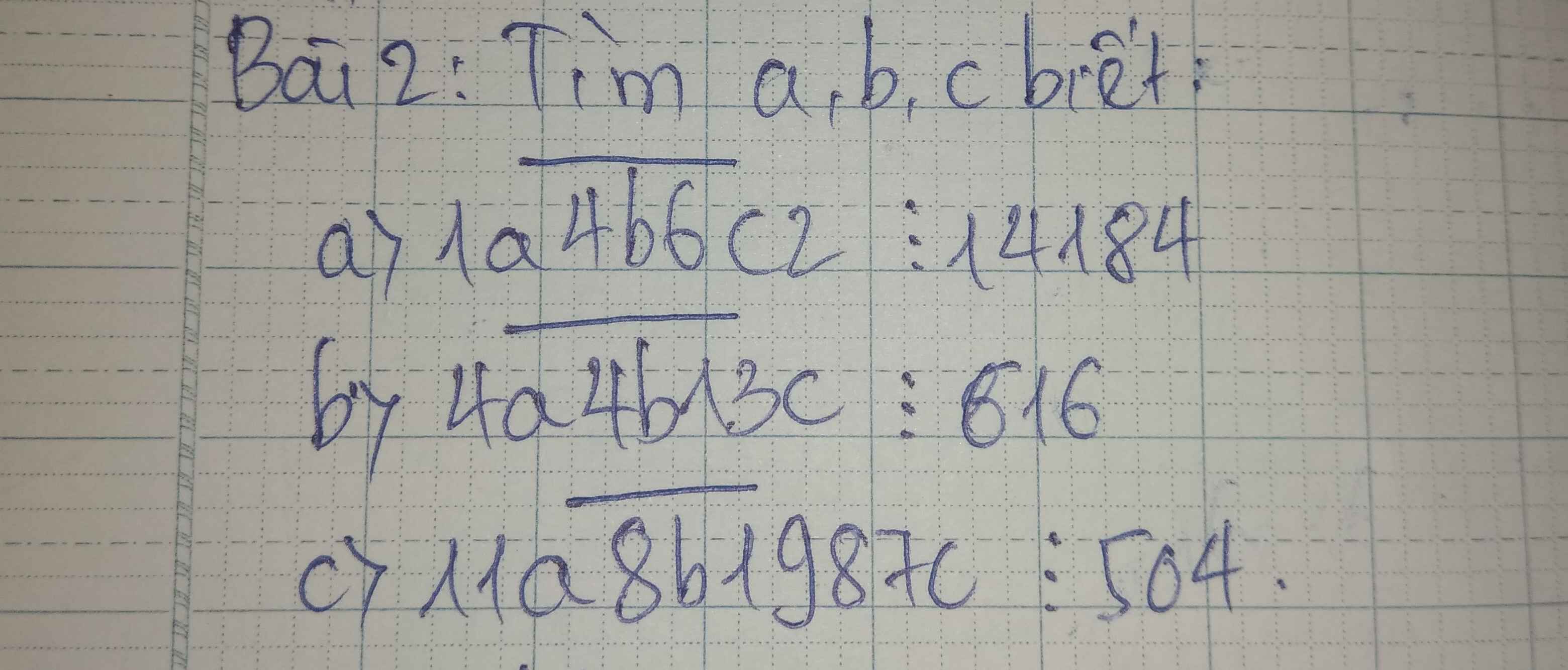
Lời giải:
a. ĐKXĐ: $x^2+5x+4\neq 0$
$\Leftrightarrow (x+1)(x+4)\neq 0$
$\Leftrightarrow x\neq -1; x\neq -4$
b. $M=\frac{x^2+4x+3}{x^2+5x+4}=\frac{(x+1)(x+3)}{(x+1)(x+4)}=\frac{x+3}{x+4}$
Tại $x=0$ thì $M=\frac{0+3}{0+4}=\frac{3}{4}$
Tại $x=2$ thì $M=\frac{2+3}{2+4}=\frac{5}{6}$
Tại $x=-3$ thì $M=\frac{-3+3}{-3+4}=0$
giải thích hộ e sao suy ra dc (x+1) (x+4) vậy ạ