
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1. a
$(3x+5)^2=(3x)^2+2.3x.5+5^2$
$=9x^2+30x+25$
1.b
$(6x^2+\frac{1}{3})^2=(6x^2)^2+2.6x^2.\frac{1}{3}+(\frac{1}{3})^2$
$=36x^4+4x^2+\frac{1}{9}$
1.c
$(5x-4y)^2=(5x)^2-2.5x.4y+(4y)^2$
$=25x^2-40xy+16y^2$
1.d
(2x^2y-3y^3x)^2=(2x^2y)^2-2.2x^2y.3y^3x+(3y^3x)^2$
$=4x^4y^2-12x^3y^4+9x^2y^6$
1.e
$(5x-3)(5x+3)=(5x)^2-3^2=25x^2-9$
1.f
$(6x+5y)(6x-5y)=(6x)^2-(5y)^2=36x^2-25y^2$
1.g
$(-4xy-5)(5-4xy)=(-4xy-5)(-4xy+5)$
$=(-4xy)^2-5^2=16x^2y^2-25$
1.h
$(a^2b+ab^2)(ab^2-a^2b)=(ab^2+a^2b)(ab^2-a^2b)$
$=(ab^2)^2-(a^2b)^2=a^2b^4-a^4b^2$
CM:(n-1)^2(n+1)+(n-1)(n+1) chia hết cho 6 với 1 số nguyên n. Mng giúp mình vs ạ. Mình c.on nhiều ạaa

\(\left(n-1\right)^2\left(n+1\right)+\left(n-1\right)\left(n+1\right)\)
\(=\left(n-1\right)\left(n+1\right)\left[\left(n-1\right)+1\right]\)
\(=\left(n-1\right)\left(n+1\right)\left(n-1+1\right)\)
\(=n\left(n-1\right)\left(n+1\right)\)
Xét:
\(n\left(n-1\right)\) là hai số tự nhiên liên tiếp nên sẽ có số chẵn nên sẽ chia hết cho 2
\(n\left(n-1\right)\left(n+1\right)\) là 3 số tự nhiên liên tiếp nên sẽ chia hết cho 3
Mà: (2;3)=1 nên
\(n\left(n-1\right)\left(n+1\right)\) sẽ chia hết cho 2 x 3 = 6 (đpcm)
\(\left(n-1\right)^2\left(n+1\right)+\left(n-1\right)\left(n+1\right)\)
\(=\left(n-1\right)\left(n+1\right)\left(n-1+1\right)\)
\(=\left(n-1\right)n\left(n+1\right)\) là 3 số tự nhiên liên tiếp
\(\Rightarrow\left\{{}\begin{matrix}\left(n-1\right)n\left(n+1\right)⋮2\\\left(n-1\right)n\left(n+1\right)⋮3\end{matrix}\right.\)
\(\Rightarrow\left(n-1\right)n\left(n+1\right)⋮\left(2.3\right)\)
mà \(UCLN\left(2;3\right)=1\)
\(\Rightarrow\left(n-1\right)n\left(n+1\right)⋮6\)
\(\Rightarrow dpcm\)


Lời giải:
Vì $D,E$ lần lượt là trung điểm $AB,AC$ nên $DE$ là đường trung bình của tam giác $ABC$ ứng với cạnh $BC$
$\Rightarrow DE\parallel BC$ và $DE=\frac{BC}{2}=2$ (cm)
Vì $DE\parallel BC$ nên $DECB$ là hình thang
Xét hình thang $DECB$ có $M,N$ lần lượt là trung điểm của cạnh bên $BD, CE$ nên $MN$ là đường trung bình của hình thang $DECB$
$\Rightarrow MN=\frac{DE+BC}{2}=\frac{2+4}{2}=3$ (cm)

a) \(\left(2x+3\right)^2-3\left(x-4\right)\left(x+4\right)=\left(x-2\right)^2+1\)
\(\Leftrightarrow4x^2+12x+9-3\left(x^2-16\right)=x^2-4x+4+1\)
\(\Leftrightarrow4x^2+12x+9-3x^2+48=x^2-4x+5\)
\(\Leftrightarrow x^2+12x+57=x^2-4x+5\)
\(\Leftrightarrow16x+52=0\)
\(\Leftrightarrow x=-\frac{13}{4}\)
b) \(\left(3x-2\right)\left(9x^2+6x+4\right)-\left(3x-1\right)\left(9x^2-3x+1\right)=x-4\)
\(\Leftrightarrow\)Xem lại đề !
c) \(x\left(x-1\right)-\left(x-3\right)\left(x+4\right)=5x\)
\(\Leftrightarrow x^2-x-x^2-x+12=5x\)
\(\Leftrightarrow-2x+12=5x\)
\(\Leftrightarrow7x-12=0\)
\(\Leftrightarrow x=\frac{12}{7}\)
d) \(\left(2x+1\right)\left(2x-1\right)=4x\left(x-7\right)-3x\)
\(\Leftrightarrow4x^2-1=4x^2-28x-3x\)
\(\Leftrightarrow28x+3x-1=0\)
\(\Leftrightarrow31x-1=0\)
\(\Leftrightarrow x=\frac{1}{31}\)


Ta có: \(7x+4=x-2m\left(1\right)\)
Thay \(x=6\) vào \(\left(1\right)\) ta có:
\(7.6+4=6-2m\)
\(\Rightarrow46=6-2m\)
\(\Rightarrow-2m=40\)
\(\Rightarrow m=-20\)

a) \(A=\left(x+5\right)^2-\left(x+3\right)^2\)
\(=\left[\left(x+5\right)-\left(x+3\right)\right]\left[\left(x+5\right)+\left(x+3\right)\right]\)
\(=\left(x+5-x-3\right)\left(x+5+x+3\right)\)
\(=2\left(2x+8\right)\)
\(=4x+16\)
b) \(B=\left(4x+1\right)^2-\left(2x+1\right)^2\)
\(=\left[\left(4x+1\right)-\left(2x+1\right)\right]\left[\left(4x+1\right)+\left(2x+1\right)\right]\)
\(=\left(4x+1-2x-1\right)\left(4x+1+2x+1\right)\)
\(=2x\left(6x+2\right)\)
\(=12x^2+4x\)
c) \(C=\left(3-4x\right)^2-\left(2x-1\right)\left(8x-9\right)\)
\(=9-24x+16x^2-16x^2+18x+8x-9\)
\(=\left(16x^2-16x^2\right)+\left(-24x+18x+8x\right)+\left(9-9\right)\)
\(=2x\)
d) \(D=\left(4+2x^2\right)-\left(1-4x\right)\left(4-x\right)\)
\(=4+2x^2-4+x+16x-4x^2\)
\(=\left(2x^2-4x^2\right)+\left(x+16x\right)+\left(4-4\right)\)
\(=-2x^2+17x\)
e) \(E=\left(2-3x\right)^2-2\left(2-3x\right)\left(3x+5\right)+\left(3x+5\right)^2\)
\(=\left(2-3x+3x+5\right)^2\)
\(=7^2\)
\(=49\)

a: Xét ΔEBF và ΔECD có
\(\widehat{EBF}=\widehat{ECD}\)(hai góc so le trong, BF//CD)
\(\widehat{BEF}=\widehat{CED}\)(hai góc đối đỉnh)
Do đó: ΔEBF~ΔECD(2)
Xét ΔEBF và ΔDAF có
\(\widehat{F}\) chung
\(\widehat{EBF}=\widehat{DAF}\)(hai góc đồng vị, BE//AD)
Do đó: ΔEBF~ΔDAF(1)
Từ (1) và (2) suy ra ΔECD~ΔDAF
b: BE+CE=BC
=>BE+4=6
=>BE=2(cm)
Xét ΔFAD có BE//AD
nên \(\dfrac{FB}{FA}=\dfrac{EB}{AD}\)
=>\(\dfrac{FB}{BF+15}=\dfrac{2}{6}=\dfrac{1}{3}\)
=>\(3BF=BF+15\)
=>2BF=15
=>BF=7,5(cm)
AF=AB+BF=15+7,5=22,5(cm)
c: Ta có: ΔECD~ΔDAF
=>\(\dfrac{EC}{DA}=\dfrac{DE}{DF}\)
=>\(EC\cdot DF=DE\cdot DA\)
Ta có: ΔECD~ΔDAF
=>\(\dfrac{CD}{AF}=\dfrac{EC}{DA}\)
=>\(EC\cdot AF=CD\cdot DA\)



 nhờ mng giúp ạ
nhờ mng giúp ạ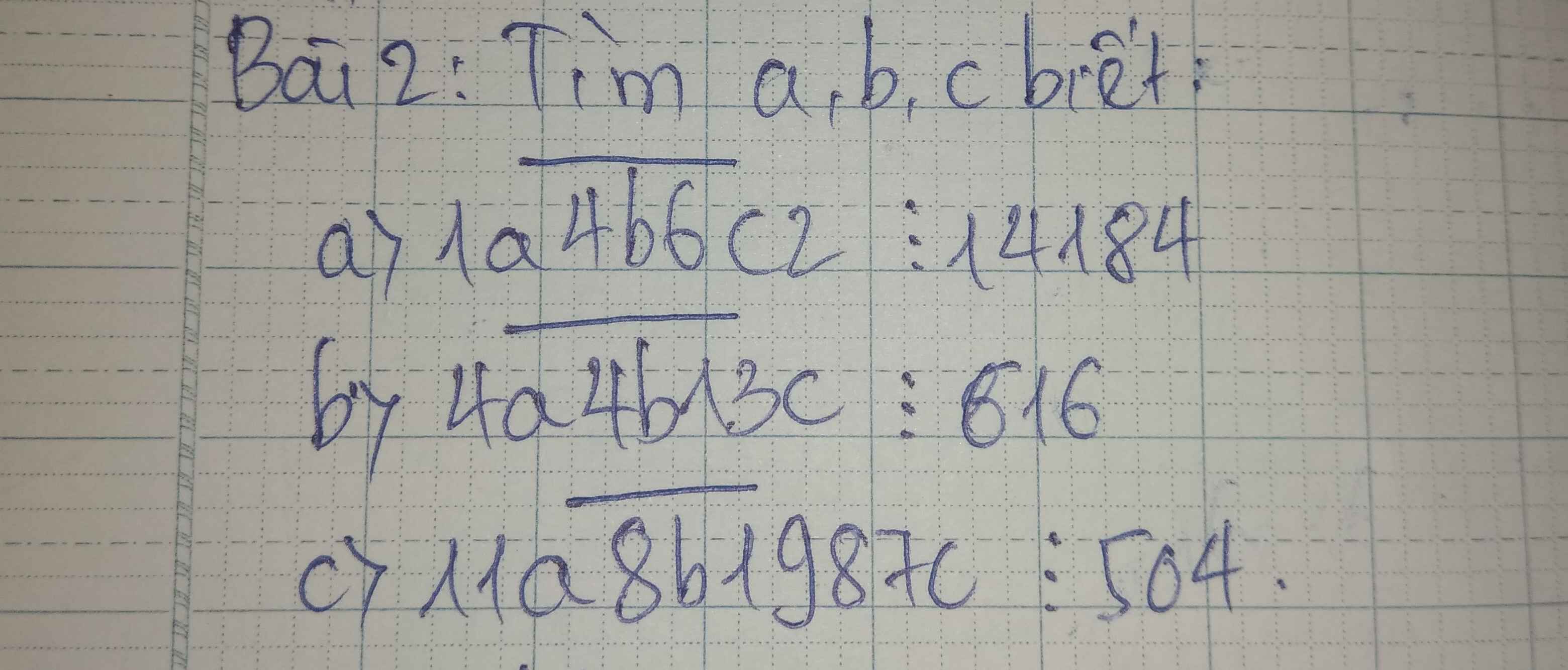

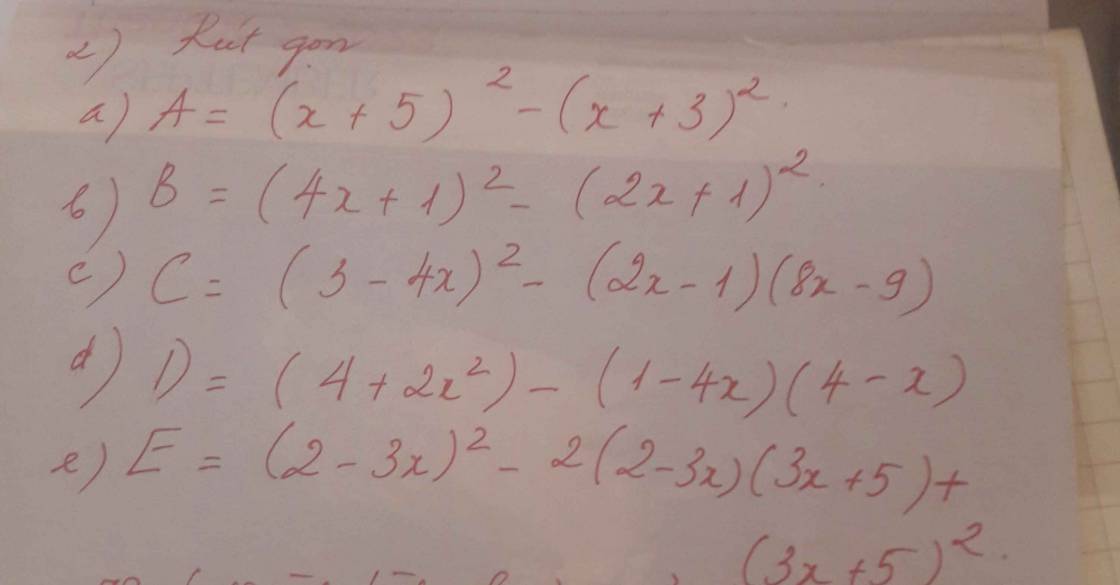

Bài 2:
a) Ta có: AB=AD(gt)
nên A nằm trên đường trung trực của BD(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: CB=CD(gt)
nên C nằm trên đường trung trực của BD(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AC là đường trung trực của BD(Đpcm)
b) Ta có: \(\widehat{BCD}=60^0\)
nên \(\widehat{CBD}=\widehat{CDB}=60^0\)
Ta có: \(\widehat{BAD}=100^0\)
nên \(\widehat{ABD}=\widehat{ADB}=\dfrac{180^0-100^0}{2}=\dfrac{80^0}{2}=40^0\)
\(\Leftrightarrow\widehat{ABC}=100^0;\widehat{ADC}=100^0\)