Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vẽ đồ thị:
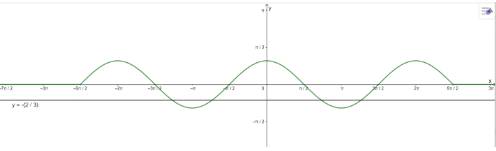
\(3\cos x + 2 = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) có 4 nghiệm

Phương trình hoàn độ giao điểm của hai đồ thì hàm số là \(\sin x = \cos x\)
\( \Leftrightarrow \tan x = 1 \Leftrightarrow x = \frac{\pi }{4} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)
Do \(x \in \left[ { - 2\pi ;\frac{{5\pi }}{2}} \right]\; \Leftrightarrow - 2\pi \le \frac{\pi }{4} + k\pi \le \frac{{5\pi }}{2}\;\; \Leftrightarrow \; - \frac{9}{4} \le k \le \frac{9}{4}\;\;\;\)
Mà \(k\; \in \mathbb{Z}\;\; \Leftrightarrow k\; \in \left\{ { - 2;\; - 1;0;1;2} \right\}\)
Vậy ta chọn đáp án A

Hàm số y = sinx đồng biến trên khoảng: \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\)
Chọn C

Ta có
\(\begin{array}{l}\sin \left( {x + \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\\ \Leftrightarrow \sin \left( {x + \frac{\pi }{4}} \right) = \sin \left( {\frac{\pi }{4}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{4}{\rm{ }} = {\rm{ }}\frac{\pi }{4} + k2\pi ;k \in Z\\x + \frac{\pi }{4}{\rm{ }} = {\rm{ }}\pi {\rm{ - }}\frac{\pi }{4} + k2\pi ;k \in Z\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = {\rm{ }}k2\pi ;k \in Z\\x{\rm{ }} = {\rm{ }}\frac{\pi }{2} + k2\pi ;k \in Z\end{array} \right.\end{array}\)
Mà \(x \in \left[ {0;\pi } \right]\) nên \(x \in \left\{ {0;\frac{\pi }{2}} \right\}\)
Vậy phương trình đã cho có số nghiệm là 2.
Chọn C

a/
\(y=\frac{1}{sinx}+\frac{1}{cosx}\ge\frac{4}{sinx+cosx}=\frac{4}{\sqrt{2}sin\left(x+\frac{\pi}{4}\right)}\ge\frac{4}{\sqrt{2}}=2\sqrt{2}\)
\(y_{min}=2\sqrt{2}\) khi \(\left\{{}\begin{matrix}sinx=cosx\\sin\left(x+\frac{\pi}{4}\right)=1\end{matrix}\right.\) \(\Rightarrow x=\frac{\pi}{4}\)
\(y_{max}\) không tồn tại (y dần tới dương vô cùng khi x gần tới 0 hoặc \(\frac{\pi}{2}\))
b/
\(y=\frac{1}{1-cosx}+\frac{1}{1+cosx}=\frac{1+cosx+1-cosx}{1-cos^2x}=\frac{2}{sin^2x}\)
Hàm số ko tồn tại cả min lẫn max ( \(0< y< \infty\))
c/
Do \(tan^2x\) ko tồn tại max (tiến tới vô cực) trên khoảng đã cho nên hàm ko tồn tại max
\(y=2+\frac{sin^4x+cos^4x}{\left(sinx.cosx\right)^2}+\frac{1}{sin^4x+cos^4x}\ge2+2\sqrt{\frac{sin^4x+cos^4x}{\frac{1}{4}sin^22x.\left(sin^4x+cos^4x\right)}}\)
\(y\ge2+\frac{4}{sin2x}\ge2+\frac{4}{1}=6\)
\(y_{min}=6\) khi \(\left\{{}\begin{matrix}sin2x=1\\sin^4x+cos^4x=sinx.cosx\end{matrix}\right.\) \(\Rightarrow x=\frac{\pi}{4}\)

\(0< \dfrac{1}{2018}< 1\)
Kẻ 1 đường thẳng nằm ngang nằm giữa \(y=0\) và \(y=1\) ta thấy cắt đồ thị tại 5 điểm trên đoạn đã cho
\(\Rightarrow\) Pt có 5 nghiệm
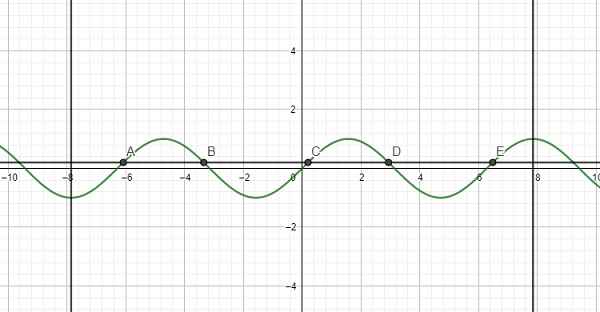

a) y = sinx
- Khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
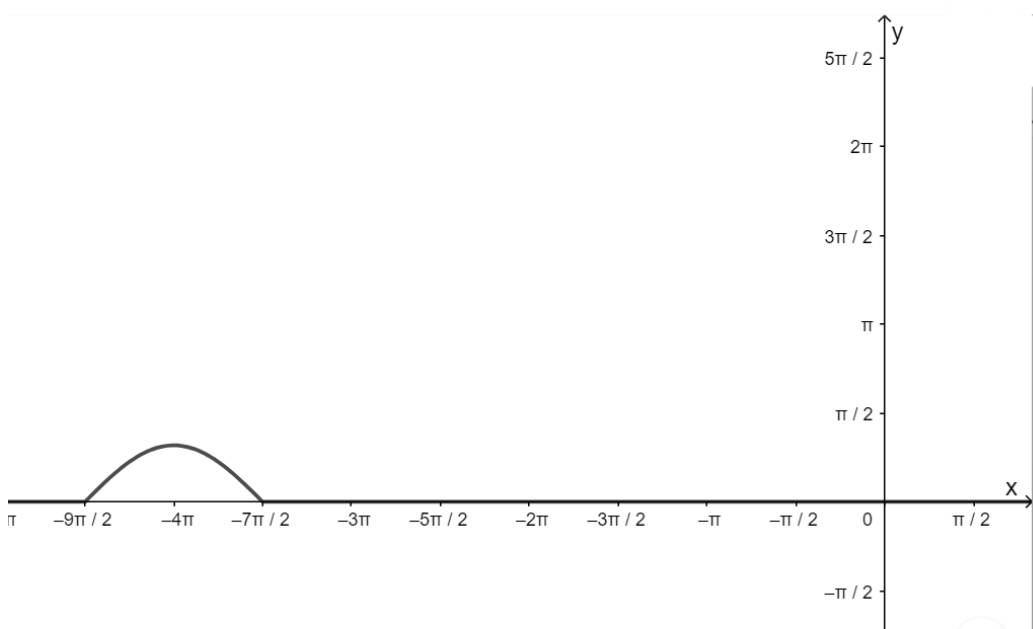
+ Đồng biến trên khoảng \(\left( { - \frac{{9\pi }}{2}; - 4\pi } \right)\)
+ Nghịch biến trên khoảng; \(\left( { - 4\pi ; - \frac{{7\pi }}{2}} \right)\)
- Khoảng \(\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
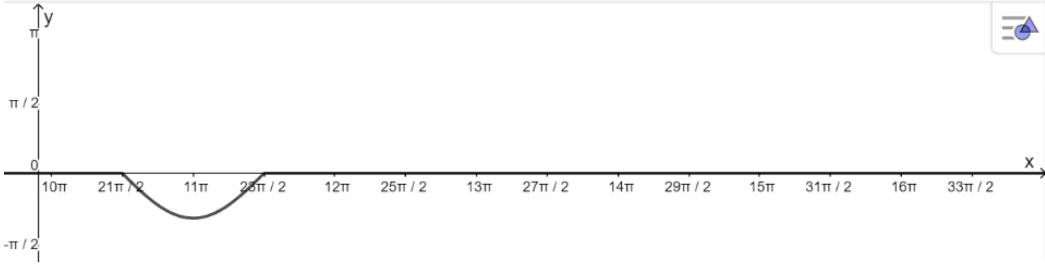
+ Đồng biến trên khoảng: \(\left( {11\pi ;\frac{{23\pi }}{2}} \right)\)
+ Nghịch biến trên khoảng: \(\left( {\frac{{21\pi }}{2};11\pi } \right)\)

Câu 2 bạn coi lại đề
3.
\(1+2sinx.cosx-2cosx+\sqrt{2}sinx+2cosx\left(1-cosx\right)=0\)
\(\Leftrightarrow sin2x-\left(2cos^2x-1\right)+\sqrt{2}sinx=0\)
\(\Leftrightarrow sin2x-cos2x=-\sqrt{2}sinx\)
\(\Leftrightarrow\sqrt{2}sin\left(2x-\frac{\pi}{4}\right)=\sqrt{2}sin\left(-x\right)\)
\(\Leftrightarrow sin\left(2x-\frac{\pi}{4}\right)=sin\left(-x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{4}=-x+k2\pi\\2x-\frac{\pi}{4}=\pi+x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
4.
Bạn coi lại đề, xuất hiện 2 số hạng \(cos4x\) ở vế trái nên chắc là bạn ghi nhầm
5.
\(\Leftrightarrow sinx.sin2x-cosx.sin^22x=2cos^2\left(\frac{\pi}{4}-x\right)-1\)
\(\Leftrightarrow sinx.sin2x-cosx.sin^22x=cos\left(\frac{\pi}{2}-2x\right)\)
\(\Leftrightarrow sinx.sin2x-cosx.sin^22x=sin2x\)
\(\Leftrightarrow sin2x\left(sinx-cosx.sin2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\Leftrightarrow x=...\\sinx-cosx.sin2x-1=0\left(1\right)\end{matrix}\right.\)
Xét (1):
\(\Leftrightarrow sinx-1-2sinx.cos^2x=0\)
\(\Leftrightarrow sinx-1-2sinx\left(1-sin^2x\right)=0\)
\(\Leftrightarrow2sin^3x-sinx-1=0\)
\(\Leftrightarrow\left(sinx-1\right)\left(2sin^2x+2sinx+1\right)=0\)
\(\Leftrightarrow...\)
a) Vẽ đồ thị:
\(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\) có 5 nghiệm
b) Vẽ đồ thị:
\(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) có 6 nghiệm