
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 9
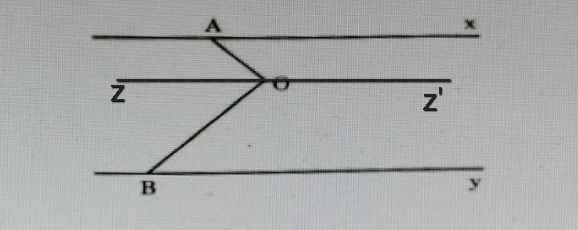
Qua O vẽ đường thẳng zz' // Ax // By
Do Ax // zz'
⇒ ∠AOz = ∠OAx = 40⁰
Do By // zz'
⇒ ∠zOB = ∠OBy = 50⁰ (so le trong)
⇒ ∠AOB = ∠AOz + ∠zOB
= 40⁰ + 50⁰
= 90⁰
Bài 10
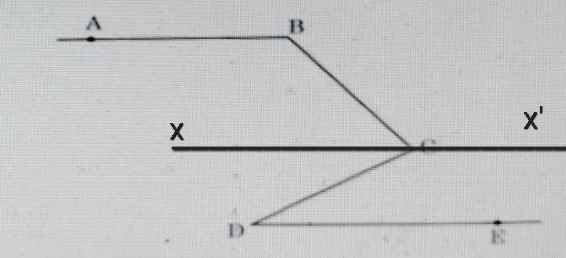 Qua C vẽ đường thẳng xx' // AB // DE
Qua C vẽ đường thẳng xx' // AB // DE
Do AB // xx'
⇒ ∠ABC = ∠BCx' = 130⁰ (so le trong)
Ta có:
∠BCx + ∠BCx' = 180⁰ (kề bù)
⇒ ∠BCx = 180⁰ - ∠BCx'
= 180⁰ - 130⁰
= 50⁰
Do DE // xx'
⇒ ∠xCD = ∠CDE = 30⁰ (so le trong)
⇒ ∠BCD = ∠BCx + ∠xCD
= 50⁰ + 30⁰
= 80⁰

Có tam giác CAB cân tại C, góc C=80*
=>góc CAB = góc CBA = (180*-80*)/2=50*
=> góc MAC = gócBAC - góc MAB = 50*-10* = 40*

Tam giác AOB cân tại O => Góc OAB = góc OBA và OA=OB
=>OA=OC do OB=OC
=>Tam giác OAC cân tại O
=>Góc OAC = góc OCA
Vậy BAC=BAO+OAC=OBA+OCA=1800-BAC
=>BAC=1800-BAC
=>2BAC=1800
=>BAC=1800/2=900

bài làm
Ta có:vì AB=AC(gt)
mà trên tia đối của AB và AC lấy điểm D và E sao cho BD=CE
=>^BDE=^CED(2 góc tương ứng)
Xét t.g BDE và t.g CED
ED là cạnh chung
BD = CE
^BDE=^CED(cmt)
=>t.g BDE=t.g CED (c.g.c)
XL mình chỉ làm đc phần a thôi ( không biết có đúng không)

Bài 3.37
a) Do BE // AC (gt)
⇒ ∠ABE = ∠A = 80⁰ (so le trong)
Do CF // AB
⇒ ∠ACF = ∠A = 80⁰ (so le trong)
⇒ ∠ABE = ∠ACF = 80⁰
b) Do CF // AB
⇒ ∠FCz = ∠ABC = 60⁰ (đồng vị)
Ta có:
∠BCF + ∠FCz = 180⁰ (kề bù)
⇒ ∠BCF = 180⁰ - ∠FCz
= 180⁰ - 60⁰
= 120⁰
⇒ ∠ACB = ∠BCF - ∠ACF
= 120⁰ - 80⁰
= 40⁰
c) Do Bx là tia phân giác của ∠ABE
⇒ ∠ABx = ∠ABE : 2 = 80⁰ : 2 = 40⁰
⇒ ∠xBC = ∠ABx + ∠ABC
= 40⁰ + 60⁰
= 100⁰
Do Cy là tia phân giác của ∠ACF
⇒ ∠yCF = ∠ACF : 2 = 80⁰ : 2 = 40⁰
⇒ ∠yCz = ∠yCF + ∠FCz
= 40⁰ + 60⁰
= 100⁰
⇒ ∠xBC = ∠yCz = 100⁰
Mà ∠xBC và ∠yCz là hai góc đồng vị
⇒ Bx // Cy
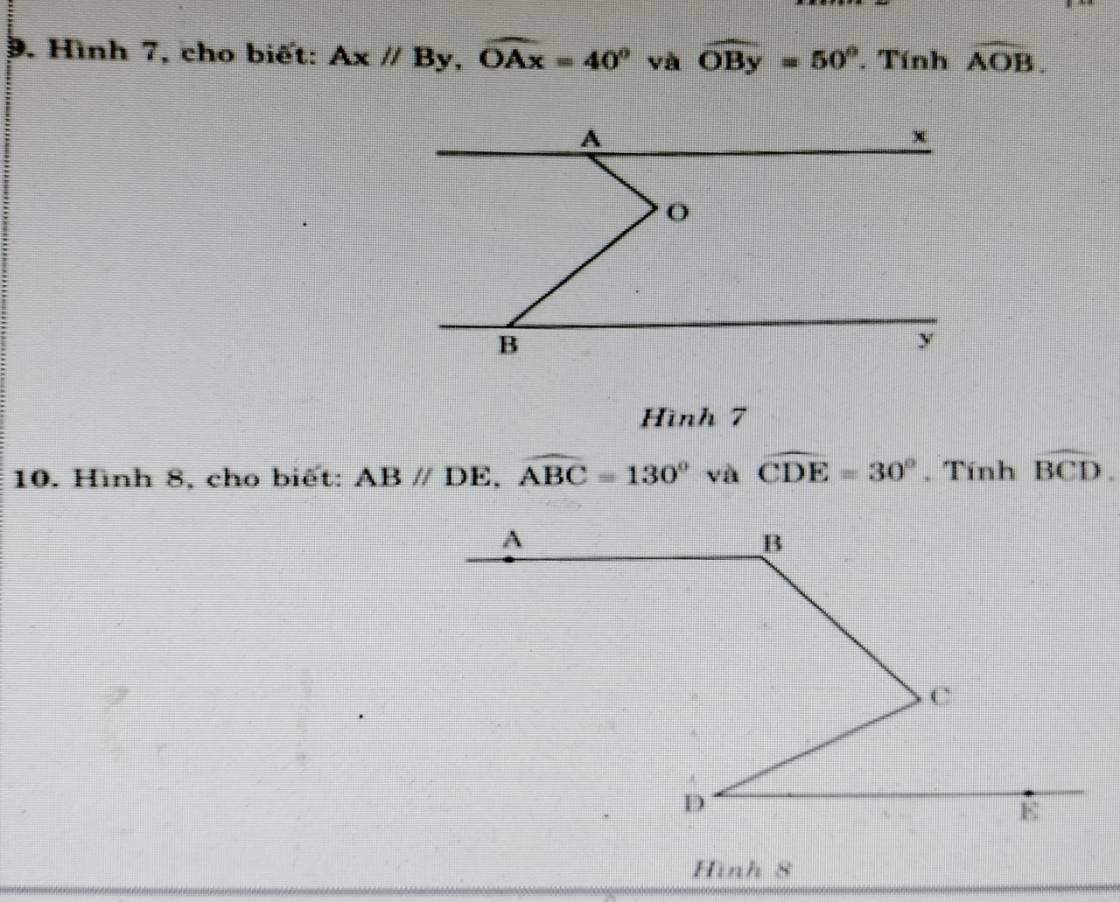
Bài 3.36
a) Do Ox // AB
⇒ ∠BOx = ∠ABO = 40⁰ (so le trong)
b) Ta có:
∠xOD = ∠BOD - ∠BOx
= 110⁰ - 40⁰
= 70⁰
⇒ ∠xOD = ∠ODC = 70⁰
Mà ∠xOD và ∠ODC là hai góc so le trong
⇒ Ox // CD
Mà Ox // AB (gt)
⇒ AB // CD
 giup em voi mn ko can ve hinh dau de em tu ve cung dc a
giup em voi mn ko can ve hinh dau de em tu ve cung dc a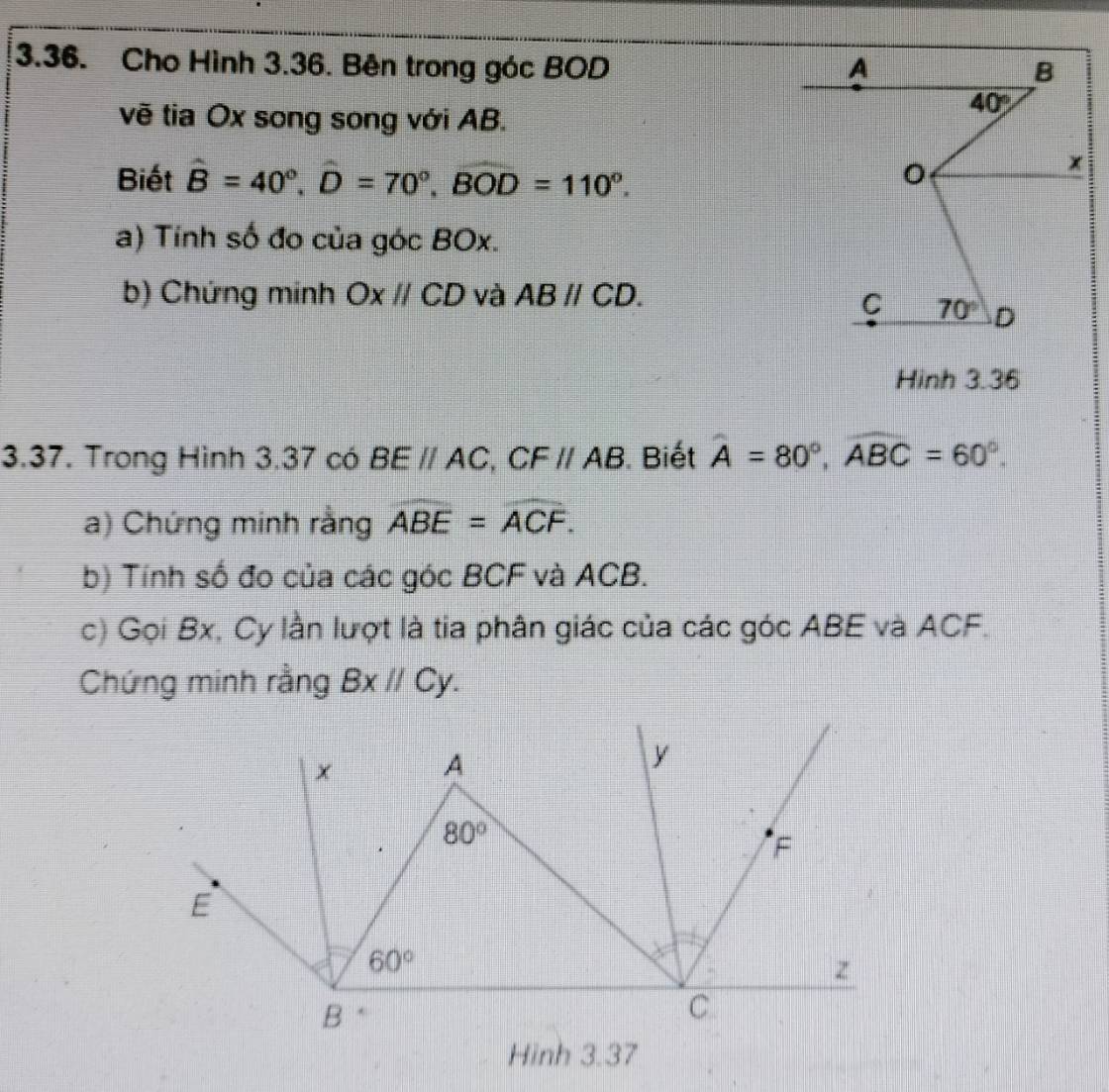 giup em dc ko a em dang can gap a ko can ve hinh dau a
giup em dc ko a em dang can gap a ko can ve hinh dau a
(√(10²-10) /10) ! = 6