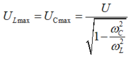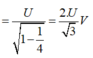Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(Z_L=40\Omega\)
\(U_L=IZ_L=\frac{U}{Z}Z_L=\frac{120.40}{\sqrt{30^2+\left(40-Z_C\right)^2}}\)
Suy ra \(U_L\)max khi \(Z_C=40\Omega\)
\(U_{Lmax}=\frac{120.40}{30}=160V\)
Đáp án C
+ Kiến thức: L của cuộn dây thay đổi, còn các đại lượng khác không đổi:
Hiệu điện thế
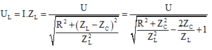
đạt cực đại khi và chỉ khi:
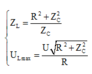
và khi đó ta có :
+ Vận dụng:
Điều chỉnh L để UL cực đại thì :
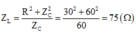
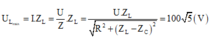
Nhận xét: Dạng bài mạch RLC có L biến thiên. Vậy khi điều chỉnh L để U L m a x thì
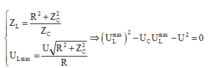
Dung kháng của tụ điện Z C = 1 C ω = 50 Ω .
→ Cảm kháng để xảy ra cực đại của điện áp hiệu dụng trên cuộn dây Z L = R 2 + Z C 2 Z C = 100 Ω → L=1/π H.
Đáp án B
Đáp án A
+ Khi xảy ra cực đại của điện áp hiệu dụng trên hai đầu cuộn dây thì ô vuông pha với 
→ Áp dụng hệ thức lượng trong tam giác, ta có
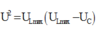
Khi U L cực đại thì điện áp tức thời giữa hai đầu đoạn mạch sẽ vuông pha với điện áp tức thời giữa hai đầu đoạn mạch chứa RC
→ U = U L m a x − U C U L m a x = 80 V.
Đáp án A
Chọn đáp án C.
Theo bài thay đổi C để 
thì I1=I2 tức là Z1=Z2, điều này suy ra
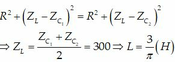
Đáp án D
Để cường độ dòng điện hiệu dụng trong mạch đạt giá trị cực đại thì mạch xảy ra hiện tượng cộng hưởng điện
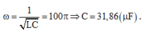
Đáp án B
Phương pháp: Điều kiện cực trị khi tần số thay đổi.
Cách giải: Khi tần số góc thay đổi thì có các giá trị để điện áp trên cuộn cảm hay tụ đạt cực đại.
Ta có:
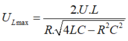
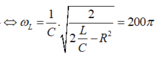
Và điện áp trên tụ cực đại là:
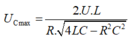
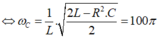
Dễ thấy:
