
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: Xét tứ giác OBPC có
\(\widehat{OBP}+\widehat{OCP}=90^0+90^0=180^0\)
=>OBPC là tứ giác nội tiếp
=>O,B,P,C cùng thuộc một đường tròn
2: Xét (O) có
PC,PB là các tiếp tuyến
Do đó: PC=PB
=>P nằm trên đường trung trực của CB(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OP là đường trung trực của BC
=>OP\(\perp\)BC
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>AC\(\perp\)CB
Ta có: AC\(\perp\)CB
OP\(\perp\)CP
Do đó: AC//OP

Học toán hình trước tiên bạn phải thuộc hết công thức tính các hình thì mới có thể giỏi toán đc.

a, Vì MA là tiếp tuyến (O) với A là tiếp điểm
=> ^MAO = 900
I là trung điểm BC => OI vuông BC
Xét tứ giác MAOI có
^MAO + MIO = 1800
mà 2 góc này đối
Vậy tứ giác MAOI là tứ giác nt 1 đường tròn
b, Xét tam giác MAB và tam giác MCA có
^M _ chung
^MAB = ^MCA ( cùng chắn cung AB )
Vậy tam giác MAB ~ tam giác MCA (g.g)
\(\dfrac{MA}{MC}=\dfrac{MB}{MA}\Rightarrow MA^2=MB.MC\)(1)
Xét tam giác MAO vuông tại A, đường cao AH
Ta có AM^2 = MH.MO ( tỉ lệ thức ) (2)
Xét tam giác MHK và tam giác MIO có
^M _ chung
^MHK = ^MIO = 900
Vậy tam giác MHK ~ tam giác MIO (g,g)
\(\dfrac{MH}{MI}=\dfrac{MK}{MO}\Rightarrow MH.MO=MK.MI\)(3)
Từ (1) ; (2) ; (3) suy ra \(MK.MI=MB.MC\)

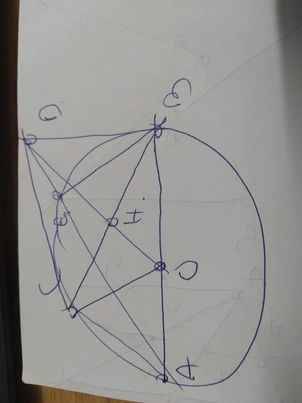
1:
Ta có;ΔCAB vuông tại C
=>ΔCAB nội tiếp đường tròn đường kính AB
mà ΔCAB nội tiếp (O)
nên O là trung điểm của AB
Xét tứ giác OBDC có
\(\widehat{OBD}+\widehat{OCD}=90^0+90^0=180^0\)
=>OBDC là tứ giác nội tiếp
=>O,B,D,C cùng thuộc một đường tròn
Xét (O) có
DB,DC là các tiếp tuyến
Do đó: DB=DC
=>D nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OD là đường trung trực của BC
=>OD\(\perp\)BC tại H và H là trung điểm của BC
Ta có: OD\(\perp\)BC
AC\(\perp\)BC
Do đó: OD//AC
2: Xét (O) có
ΔBEA nội tiếp
BA là đường kính
Do đó: ΔBEA vuông tại E
=>BE\(\perp\)EA tại E
=>BE\(\perp\)AD tại E
Xét ΔBAD vuông tại B có BE là đường cao
nên \(DE\cdot DA=DB^2\left(3\right)\)
Xét ΔDBO vuông tại B có BH là đường cao
nên \(DH\cdot DO=DB^2\left(4\right)\)
Từ (3) và (4) suy ra \(DE\cdot DA=DH\cdot DO\)

Lời giải:
Diện tích xung quanh của hình nón là:
$S_{xq}=\pi rl =3,14.7.11=241,78$ (cm2)

Bạn lấy điểm E là trung điểm của OA, xong vẽ đường tròn bán kính AE cắt (O) tại B,C; nối hai đường AB,AC, ta được AB,AC là các tiếp tuyến cần vẽ

a: Xét (O) có
ΔAKB nội tiếp
AB là đường kính
Do đó: ΔAKB vuông tại K
Xét tứ giác EMBK có \(\widehat{EMB}+\widehat{EKB}=90^0+90^0=180^0\)
nên EMBK là tứ giác nội tiếp
b: Xét (O) có
OA là bán kính
OA\(\perp\)CD tại M
Do đó: \(sđ\stackrel\frown{AC}=sđ\stackrel\frown{AD}\)
Xét (O) có
\(\widehat{AKC}\) là góc nội tiếp chắn cung AC
\(\widehat{ACD}\) là góc nội tiếp chắn cung AD
\(sđ\stackrel\frown{AD}=sđ\stackrel\frown{AC}\)
Do đó: \(\widehat{AKC}=\widehat{ACD}\)
Xét ΔAKC và ΔACE có
\(\widehat{AKC}=\widehat{ACE}\)
\(\widehat{KAC}\) chung
Do đó: ΔAKC đồng dạng với ΔACE
=>\(\dfrac{AK}{AC}=\dfrac{AC}{AE}\)
=>\(AE\cdot AK=AC^2\)
 có vẽ hình lun ạ
có vẽ hình lun ạ

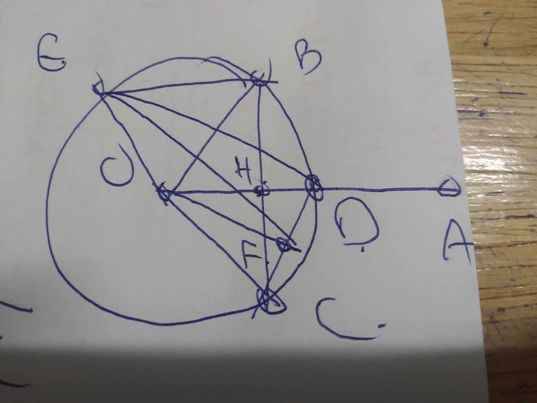





1:
Ta có: ΔABC vuông tại C
mà ΔCAB nội tiếp (O)
nên O là trung điểm của AB
Xét tứ giác OBDC có \(\widehat{OBD}+\widehat{OCD}=90^0+90^0=180^0\)
nên OBDC là tứ giác nội tiếp
=>O,B,D,C cùng thuộc một đường tròn
Xét (O) có
DC,DB là các tiếp tuyến
Do đó: DC=DB
=>D nằm trên đường trung trực của CB(1)
Ta có: OC=OB
=>O nằm trên đường trung trực của CB(2)
Từ (1) và (2) suy ra OD là đường trung trực của CB
=>OD\(\perp\)CB
Ta có: AC\(\perp\)CB
CB\(\perp\)OD
Do đó: OD//AC
2: Xét (O) có
ΔBEA nội tiếp
AB là đường kính
Do đó: ΔBAE vuông tại E
=>BE\(\perp\)EA tại E
=>BE\(\perp\)AD tại E
Xét ΔBAD vuông tại B có BE là đường cao
nên \(DE\cdot DA=DB^2\left(3\right)\)
Xét ΔDOB vuông tại B có BH là đường cao
nên \(DH\cdot DO=DB^2\)(4)
Từ (3) và (4) suy ra \(DE\cdot DA=DH\cdot DO\)