Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(R_{Đ1}=\dfrac{U^2_{Đ1}}{P_{Đ1}}=\dfrac{220^2}{100}=484\Omega\)
\(R_{Đ2}=\dfrac{U^2_{Đ2}}{P_{Đ2}}=\dfrac{220^2}{40}=1210\Omega\)
\(I_{Đ1đm}=\dfrac{P_{Đ1}}{U_{Đ1}}=\dfrac{100}{220}=\dfrac{5}{11}A\)
\(I_{Đ2đm}=\dfrac{P_{Đ2}}{U_{Đ2}}=\dfrac{40}{220}=\dfrac{2}{11}A\)
a)Mắc song song:
\(U_1=U_2=U=220V\)
\(I_{Đ1}=\dfrac{U_1}{R_1}=\dfrac{220}{484}=\dfrac{5}{11}A=I_{Đ1đm}\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{220}{1210}=\dfrac{2}{11}A=I_{Đ2đm}\)
\(\Rightarrow I_1>I_2\Rightarrow\)Đèn 1 sáng hơn.
b)Mắc nối tiếp:
\(R=R_1+R_2=484+1210=1694\Omega\)
\(I_1=I_2=I=\dfrac{U}{R}=\dfrac{220}{1694}=\dfrac{10}{77}A\)

Lập tỉ lệ: R 2 / R 1 = 1210 / 484 = 2,5 ⇒ R 2 = 2,5 R 1 . Vậy đèn 1 có điện trở nhỏ hơn đèn 2 là 2,5 lần.
Cường độ dòng điện định mức của đèn 1 là:
I đ m 1 = P đ m 1 / U đ m 1 = 100/220 ≈ 0,45A
+ Cường độ dòng điện định mức của đèn 2 là:
I đ m 2 = P đ m 2 / U đ m 2 = 40/220 ≈ 0,18A
Khi ghép nối tiếp cường độ dòng điện trong đoạn mạch là:
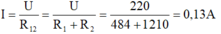
Vì đèn 1 và đèn 2 mắc nối tiếp nên: I 1 = I 2 = I = 0,13A.
Qua kết quả tính toán ta so sánh và biết được cả hai đèn thì dòng điện qua chưa đến giá trị định mức vì vậy cả hai đèn đều sáng mờ. Nhưng đèn 2 sẽ sáng hơn đèn 1. (vì I gần với I đ m 1 hơn I đ m 2 )
Điện năng tiêu thụ của đoạn mạch trong 1 giờ là:
A = U.I.t = 220.0,13.3600 = 102960 J = 0,0286kW.h
Điện năng mạch điện tiêu thụ trong 1 giờ là:
A = ( P 1 + P 2 )t = (100 + 40).3600 = 504000J = 0,14kW.h.

\(\left[{}\begin{matrix}I1=P1:U1=100:220=\dfrac{5}{11}A\\I2=P2:U2=40:220=\dfrac{2}{11}A\end{matrix}\right.\)
\(P1>P2\Rightarrow\) đèn 1 sáng hơn.
\(A=UIt=220.\left(\dfrac{5}{11}+\dfrac{2}{11}\right).2=280\)(Wh) = 0,28(kWh)

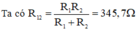
Cường độ dòng điện trong đoạn mạch là:
I = U / R 12 = 220 / 345,7 = 0,63A.
Vì đèn 1 song song với đèn 2 nên I = I 1 + I 2 = 0,63A
Ta thấy I đ m 1 + I đ m 2 = 0,45 + 0,18 = 0,63A
Nên lúc này hai đèn sáng bình thường và đèn 1 sáng hơn đèn 2 vì đèn 1 có công suất định mức lớn hơn đèn 2

a. \(p_1< p_2\left(60< 100\right)\). Vậy đèn 2 sáng hơn.
b. \(\left\{{}\begin{matrix}R1=U1^2:P1=220^2:60\approx806,7\Omega\\R2=U2^2:P2=220^2:100=484\Omega\end{matrix}\right.\)
c. \(R=\dfrac{R1\cdot R2}{R1+R2}=\dfrac{806,7\cdot484}{806,7+484}\approx302,5\Omega\)
d. \(\left\{{}\begin{matrix}I1=P1:U1=60:220=\dfrac{3}{11}A\\I2=P2:U2=100:220=\dfrac{5}{11}A\end{matrix}\right.\)
e. \(\left\{{}\begin{matrix}Q_{toa1}=A_1=U1\cdot I1\cdot t=220\cdot\dfrac{3}{11}\cdot10\cdot60=36000\left(J\right)\\Q_{toa2}=A_2=U2\cdot I2\cdot t=220\cdot\dfrac{5}{11}\cdot10\cdot60=60000\left(J\right)\end{matrix}\right.\)
f. \(\left\{{}\begin{matrix}A1'=UI\cdot I1\cdot t=220\cdot\dfrac{3}{11}\cdot4=240\\A2'=U2\cdot I2\cdot t=220\cdot\dfrac{5}{11}\cdot4=400\end{matrix}\right.\)(W)
g. \(\left\{{}\begin{matrix}T1=A1'\cdot80=\left(240:1000\right)\cdot80=19,2\left(dong\right)\\T2=A2'\cdot80=\left(400:1000\right)\cdot80=32\left(dong\right)\end{matrix}\right.\)
\(T=T1+T2=19,2+32=51,2\left(dong\right)\)

a. \(P=P1+P2=100+75=175\left(W\right)\)
\(I=I1+I2=\left(\dfrac{P1}{U1}\right)+\left(\dfrac{P2}{U2}\right)=\left(\dfrac{100}{220}\right)+\left(\dfrac{75}{220}\right)=\dfrac{35}{44}\left(A\right)\)(R1//R2)
b. \(I=I1=I2=\dfrac{U}{R}=\dfrac{220}{\left(\dfrac{220^2}{100}\right)+\left(\dfrac{220^2}{75}\right)}=\dfrac{15}{77}A\left(R1ntR2\right)\)
\(\left\{{}\begin{matrix}U1=I1.R1=\dfrac{15}{77}.\left(\dfrac{U1^2}{P1}\right)=\dfrac{15}{77}.\left(\dfrac{220^2}{100}\right)=\dfrac{660}{7}V\\U2=I2.R2=\dfrac{15}{77}.\left(\dfrac{U2^2}{P2}\right)=\dfrac{15}{77}.\left(\dfrac{220^2}{75}\right)=\dfrac{880}{7}V\end{matrix}\right.\)
\(P_{nt}=U_{nt}.I_{nt}=220.\dfrac{15}{77}=\dfrac{300}{7}\left(W\right)\)

\(I=I1+I2=\left(\dfrac{P1}{U1}\right)+\left(\dfrac{P2}{U2}\right)=\left(\dfrac{100}{220}\right)+\left(\dfrac{25}{220}\right)=\dfrac{25}{44}A\)
\(\Rightarrow A=UIt=220.\dfrac{25}{44}.4=500\left(Wh\right)=0,5\left(kWh\right)=1800000\left(J\right)\)

