Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Gọi A là biến cố “Cú sút đó không vào lưới”. Nếu cầu thủ sút vào vị trí 1 hoặc 2, xác suất để bóng không vào bằng 2 1 4 . 1 4 = 1 8 . Nếu cầu thủ sút cào vị trí 3 hoặc 4, xác suất để bóng không vào bằng 2 1 4 . 1 4 . 1 2 = 1 16 . Suy ra xác suất để bóng không vào bằng P A = 1 8 + 1 16 = 3 16 .

Gọi tên hai cầu thủ ghi bàn là A và B.
Cứ mỗi vị trí ngồi của A có đúng một cách sắp xếp A-B. Vì A có 10 vị trí ngồi nên có 10 cách sắp xếp. Chọn A.
Chú ý. Đề chỉ quan tâm đến hai cầu thủ ghi bàn và cách xếp hai cầu thủ này ngồi đối diện trong bàn tròn có 10 chỗ ngồi.

Chọn đáp án A
Gọi Ai là biến cố “cầu thủ thứ I ghi bàn” với i ∈ 1 ; 2 ; 3 .
Các biến cố Ai độc lập với nhau và P(A1) = x; P(A2) = y; P(A3) = 0,6.
* Gọi A là biến cố “Có ít nhất một trong ba cầu thủ ghi bàn” P(A) = 0,976.
Ta có là biến cố “không có cầu thủ nào ghi bàn”.
![]()
![]()
Ta có phương trình
![]()
* Gọi B là biến cố “Cả ba cầu thủ đều ghi bàn” P(B) = 0,336.
Mặt khác P(B) = P(A1).P(A2).P(A3) = 0,6xy.
Ta có phương trình
![]()
* Từ (1) và (2) ta có hệ phương trình
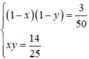

Suy ra x, y là nghiệm của phương trình
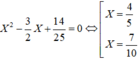
Do x > y nên x = 4 5 = 0 , 8 và y = 7 10 = 0 , 7 .
* Gọi C là biến cố “Có đúng hai cầu thủ ghi bàn”
Khi đó
![]()
⇒ P C = 0 , 452

Đáp án B
Số cách sắp ngẫu nhiên là C 9 3 C 6 3 C 3 3 = 1680 (cách)
Số cách sắp để ba đội của Việt Nam ở 3 bảng khác nhau là: C 6 2 C 3 1 C 4 2 C 2 1 C 2 2 C 1 2 = 540 (cách)
Xác suất để 3 đội bóng của Việt Nam ở 3 bảng khác nhau là: 540 1680 = 9 28

CÓ ÍT NHẤT 1 cầu thủ ghi bàn có 2 cách làm
cách thứ nhất:
có ít nhất 1 cầu thủ ghi bàn có 3 trường hợp xảy ra là: cầu thủ 1 ghi bàn cầu thủ 2 không ghi bàn, cầu thủ 2 ghi bàn cầu thủ 1 không ghi bàn, và cả 2 cầu thủ ghi bàn
suy ra sx bằng: 0.8.0,3+0,7.0,2+0,7.,8
cách thứ 2 là : sử dụng biến cố đối
A: không có cầu thủ nào ghi bàn
với P(A)=0,2.0,3
B" có ít nhất 1 cầu thủ ghi bàn"
P(B)=1-P(A)=1-0,2.0,3

Đáp án A.
Không gian mẫu là số cách chia tùy ý 12 đội thành 3 bảng.
Suy ra số phần tử của không gian mẫu là n Ω = C 12 4 . C 8 4 . C 4 4 .
Gọi X là biến cố “3 đội bóng của Việt Nam ở 3 bảng khác nhau”
Bước 1: Xếp 3 đội Việt Nam ở 3 bảng khác nhau nên có 3! cách.
Bước 2: Xếp 6 đội còn lại vào 3 bảng A, B, C này có C 9 3 . C 6 3 . C 3 3 .
Suy ra số phần tử của biến cố X là n X = 3 ! . C 9 3 . C 6 3 . C 3 3 .
Vậy xác suất cần tính là P = n X n Ω = 3 ! . C 9 3 . C 6 3 . C 3 3 C 12 4 . C 8 4 . C 4 4 = 16 55 .

Đáp án A.
Không gian mẫu là số cách chia tùy ý 12 đội thành 3 bảng.
Suy ra số phần tử của không gian mẫu là n Ω = C 12 4 . C 8 4 . C 4 4 .
Gọi X là biến cố “3 đội bóng của Việt Nam ở 3 bảng khác nhau”
Bước 1: Xếp 3 đội Việt Nam ở 3 bảng khác nhau nên có 3! cách.
Bước 2: Xếp 6 đội còn lại vào 3 bảng A, B, C này có C 9 3 . C 6 3 . C 3 3 .
Suy ra số phần tử của biến cố X là n X = 3 ! . C 9 3 . C 6 3 . C 3 3 .
Vậy xác suất cần tính là P = n X n Ω = 3 ! . C 9 3 . C 6 3 . C 3 3 C 12 4 . C 8 4 . C 4 4 = 16 55 .

Đáp án C
Cách chia 9 đội ra thành 3 bảng là:
C 9 3 C 6 3 C 3 3 = 1680
Cách chia 3 đội bóng của Việt Nam ở 3 bảng khác nhau là: C 3 1 C 6 2 C 2 1 C 4 2 = 540
⇒ p = 540 1680 = 9 28


Chọn 3 đội, mỗi đội chọn 1 cầu thủ sẽ thỏa yêu cầu bài toán.
• Có C 4 3 cách chọn 3 đội.
• Có 2 3 cách chọn 3 cầu thủ từ ba đội đó (vì mỗi cầu thủ có 2 cách chọn).
Vậy có C 4 3 8 = 32 cách chọn thỏa yêu cầu bài toán.
Chọn C.
Cách 2. Có thể tính bằng phần bù: