

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có ![]()
Do đó hàm số f(x) đồng biến trên R. Với một hàm số f(x) đồng biến trên R ta có tính chất sau:
![]() Thật vậy
Thật vậy
+) Nếu ![]()
![]() (vô lí);
(vô lí);
+) Nếu ![]()
![]() (vô lí).
(vô lí).
+) Nếu ![]()
![]() (thỏa mãn)/
(thỏa mãn)/
Từ ba khả năng trên ta có điều phải chứng minh. Áp dụng tính chất này ta có:
![]()
![]()
![]()
Phương trình đã cho có ba nghiệm thực phân biệt khi và chỉ khi (*) có ba nghiệm thực phân biệt
![]()
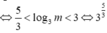
![]()
Có tất cả 20 số nguyên thỏa mãn.
Chọn đáp án A.

Đặt t = 2 x t > 0 phương trình trở thành:
![]()
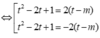
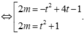
Vẽ trên cùng hệ trục toạ độ hai parabol
P 1 : y = x 2 + 1 ; ( P 2 ) : y = - x 2 + 4 x - 1 .
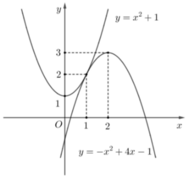
Với mỗi t > 0 cho ta một nghiệm x = log 2 t . Do đó phương trình có đúng 2 nghiệm thực phân biệt khi và chỉ khi hệ phương trình cuối có đúng 2 nghiệm dương phân biệt. Điều này tương đương với đường thẳng y = 2m cắt đồng thời (P1), (P2) tại đúng 2 điểm có hoành độ dương. Quan sát đồ thị suy ra các giá trị cần tìm của tham số là
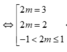
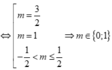
Chọn đáp án A.