Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

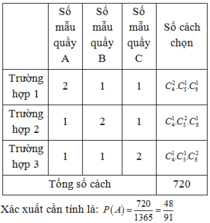
Đáp án C
Lấy 4 mẫu thịt lợn trong 15 mẫu có C 15 4 = 1365 cách
Gọi A là biến cô “mẫu thịt của cả 3 mẫu A, B, C đều được chọn”
Khi đó Ω A = C 4 2 . C 5 1 . C 6 1 + C 4 1 . C 5 2 . C 6 1 + C 4 1 . C 5 1 . C 6 2 = 720 cách

a/ Số học sinh khá bằng 3/5 số họ sinh cò lại hay bằng 3/8 tổng số họ sinh
b/Số học sinh khá chiếm:
3/5 x (1- 4/5) = 3/25 (tổng số học sinh)
Số học sinh trung bình và yếu chiếm:
1 -( 3/25 + 4/5)=2/25
Tổng số học sinh cả trường là:
60 : 2/25 = 750(học sinh)
c/ Số học sinh giỏi là:
750 . 4/5 = 600 (học sinh)
Số học sinh khá là:
750. 3/25 = 90 (học sinh)
Tỉ số giữa học sinh giỏi và khá là:
600 : 90 = 20/3

Đáp án B.
Không gian mẫu: Số cách chia 15 học sinh thành 5 nhóm, mỗi nhóm 3 học sinh:
n Ω = C 15 3 . C 12 3 . C 9 3 . C 6 3 . C 3 3 5 ! = 1401400.
Vì cả 5 nhóm đều có học sinh giỏi và khá nên sẽ có đúng 1 nhóm có 2 học sinh giỏi, 1 học
sinh khá, các nhóm còn lại đều có 1 giỏi, 1 khá và 1 trung bình.
Số kết quả thỏa mãn:
n P = C 6 2 . C 5 1 .4 ! .4 ! = 43200.
Xác suất cần tính:
n P n Ω = 216 7007 .

Chọn C.
Chọn ngẫu nhiên 6 học sinh trong 15 học sinh có C 15 6 cách ⇒ n Ω = C 16 5 .
Gọi X là biến cố “6 học sinh được chọn có đủ 3 khối” => biến cố đối X ¯ là “6 học sinh được chọn trong một khối hoặc hai khối”. Ta xét các trường hợp sau:
TH1. Chọn 6 học sinh từ một khối. Ta xét các trường hợp sau:
TH2. Chọn 6 học sinh từ hai khối, ta được
· 6 học sinh chọn từ khối 11 và 11 => có C 11 6 - C 6 6 cách
· 6 học sinh chọn từ khối 11 và 12 => có C 9 6 cách
· 6 học sinh chọn từ khối 12 và 10 => có C 10 6 - C 6 6 cách.
Vậy P = 1 - n X ¯ n Ω = 1 - 755 C 15 6 = 850 1001 .

Số cách xếp ngẫu nhiên 12 học sinh thành hàng ngang là 12! cách.
Ta tìm số cách xếp thoả mãn:
Xếp hai bạn An và Bình cạnh nhau có 2! cách, gọi nhóm này là X;
Xếp 4 bạn lớp C còn lại cùng với X có 5! cách;
Lúc này có 4 vị trí (xen giữa các bạn lớp C còn lại và X) để xếp 3 bạn lớp B vào có A34A43cách;
Còn lại 3 vị trí để các bạn lớp A có thể xếp vào (1 vị trí xen giữa và ở hai đầu) có 3.3.3 cách.
Vậy có tất cả 2 ! 5 ! A 4 3 27 cách xếp thoả mãn.
Xác suất cần tính bằng 2 ! 5 ! A 4 3 27 12 ! = 1 3080
Chọn đáp án D.





Đáp án B
Phương pháp giải: Áp dụng các quy tắm đếm cơ bản
Lời giải:
Một người có 6 cách chọn quầy khác nhau => Số phần tử của không gian mẫu là n ( Ω ) = 6 5
Chọn 3 học sinh trong 5 học sinh có C 5 3 cách, chọn 1 quầy trong 6 quầy có C 6 1 cách.
Suy ra có C 5 3 . C 6 1 cách chọn 3 học sinh vào 1 quầy bất kì.
Khi đó, 2 học sinh còn lại sẽ chọn 5 quầy còn lại => có C 5 1 cách.
Do đó, số kết quả thuận lợi cho biến cố là n(X) = C 5 1 . C 5 3 . C 6 1
Vậy P =