Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Số vòng đấu là 
vòng đấu (gồm cả lượt đi và về)
Mỗi vòng đấu có 7 trận đấu
Do đó có tất cả 
trận đấu
Đáp án B.
Tổng số trận đấu trong giải đấu là: 
Sau mỗi trận hòa, tổng số điểm 2 đội nhận được là 1.2 =2.
Sau mỗi trận không hòa, tổng số điểm 2 đội nhận được là 3 + 0 = 3.
Tổng số điểm của tất cả các đội sau khi kết thúc giải đấu là:
65.2 + (182 – 65).3 = 481.
Đáp án C
Do thi đấu vòng tròn 1lượt nên 2 đột bất kỳ chỉ đấu với nhau đúng 1 trận. Số trận đấu của giải là 
Tổng số điểm của 2 đội trong 1 trận hòa là 2 nên tổng số điểm của 23 trận hòa là 
Tổng số điểm của 2 đội trong 1 trận không hòa là 3 nên tổng số điểm của 68 trận không hòa là 
Vậy số điểm trung bình của 1 trận là 
(điểm)
Chọn D
Nhận định bài toán:
1) Đây là dạng bài toán phân chia một tập hợp ra thành các nhóm có số lượng bằng nhau.
2) Phương pháp:
Dạng bài toán này được phân chia làm 2 loại đó là:
- Các nhóm có thứ tự A, B, C, D…
- Các nhóm không phân biệt thứ tự.
Nếu không phân biệt rõ ràng 2 bài toán này thì rất dễ dẫn đến nhầm lẫn và sai kết quả.
Ví dụ: Có bao nhiêu cách chia 20 người thành 4 nhóm, mỗi nhóm có 5 người trong các trường hợp sau:
a) Các nhóm được đánh tên theo thứ tự A, B, C, D.
b) Không phân biệt thứ tự nhóm.
Lời giải
a) Số cách chọn 5 người cho nhóm A là C 20 5 . Ứng với mỗi cách chọn trên, ta có số cách chọn 5 người cho nhóm B là C 15 5 , nhóm C là C 10 5 và 5 người còn lại vào nhóm D.
Theo quy tắc nhân, ta được số cách chia nhóm là: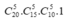 
(cách).
b) Vì các nhóm không phân biệt thứ tự nên khi ta hoán vị 4 nhóm trên sẽ cho cùng một kết quả. Do đó số cách chia trong trường hợp này là
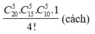
3) Phân tích bài toán và lời giải.
Chia 8 đội thành hai bảng đấu, do đó hai bảng đấu này sẽ có thứ tự rõ ràng cho nên bài toán của chúng ta thuộc loại chia nhóm có thứ tự.
Gọi hai bảng đấu là bảng A và bảng B.
Chọn 4 đội vào bảng A ta có C 8 4 cách, bốn đội còn lại vào bảng B có 1 cách.
Theo quy tắc nhân, ta có số cách chia 8 đội vào hai bảng đấu là:
Gọi A là biến cố “Hai đội Việt Nam nằm ở hai bảng khác nhau”.
Bảng A: Có 3 đội nước ngoài và 1 đội Việt Nam. Số cách chọn là C 6 3 . C 2 1 .
Bảng B: Chỉ còn 1 cách chọn duy nhất cho 3 đội nước ngoài và 1 đội Việt Nam còn lại vào bảng B.
Do đó số cách chia 8 đội thành 2 bảng mỗi bảng có 1 đội Việt Nam là : n(A) = C 6 3 . C 2 1 .1 = 40 cách
Vậy xác suất của biến cố A là: 
Chọn D
Gọi A là biến cố “3 đội của Việt Nam cùng nằm ở một bảng đấu”.
Ta có 
Chọn ra 3 đội của Việt Nam và 1 đội khác rồi xếp chung vào 1 trong 3 bảng có: 3. C 9 1 (cách).
Chọn ra 4 đội trong 8 đội còn lại để được bảng tiếp theo có: C 8 4 (cách).
Bảng còn lại có 1 cách chọn.
Chọn A
Gọi ba bảng đấu có tên là A, B, C.
Chọn 4 đội cho bảng A có C 12 4 cách, chọn 4 đội cho bảng B có C 8 4 cách và 4 đội còn lại vào bảng C có 1 cách.
Theo quy tắc nhân, số cách chia 12 đội thành 3 bảng đấu là: (cách)
Gọi A là biến cố “3 đội Việt Nam cùng nằm ở một bảng đấu.
Giả sử 3 đội Việt Nam cùng nằm ở bảng A.
Khi đó bảng A sẽ chọn 1 đội trong 9 đội nước ngoài và 3 đội Việt Nam, 8 đội còn lại chia vào bảng B và C. Trong trường hợp này ta có số cách chọn là 
Vì vai trò của các bảng là như nhau nên trường hợp 3 đội Việt Nam ở bảng B hay bảng C đều cho kết quả như nhau.
Vậy số kết quả thuận lợi cho biến cố A là 
Xác suất của biến cố A là :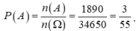 
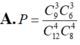
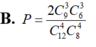
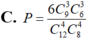
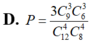
Số trận đấu sao cho hai đội bất kì trong 16 đội tham gia gặp nhau đúng một lần là:
C 16 2 = 120 trận