Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(x-y\right)^3+4y\left(2x^2+y^2\right)=\left(x+y\right)^3+2y\left(x^2+y^2\right)\)
\(\Leftrightarrow x^3-3x^2y+3xy^2-y^3+8x^2y+4y^3=x^3+3x^2y+3xy^2+y^3+2x^2y+2y^3\)
\(\Leftrightarrow\left(-3x^2y+8x^2y\right)+3xy^2+3y^3=\left(3x^2y+2x^2y\right)+3xy^2+3y^2\)
\(\Leftrightarrow5x^2y+3xy^2+3y^2=5x^2y+3xy^2+3y^2\)

a) \(VT=\left(x-1\right)\left(x^2+x+1\right)\)
\(=x^3+x^2+x-x^2-x-1\)
\(=x^3-1=VP\)
b) \(VT=\left(x^3+x^2y+xy^2+y^3\right)\left(x-y\right)\)
\(=x^4+x^3y+x^2y^2+xy^3-x^3y-x^2y^2-xy^3-y^4\)
\(=x^4-y^4=VP\)
c) \(VT=\left(x+y+z\right)^2\)
\(=\left(x+y\right)^2+2\left(x+y\right)z+z^2\)
\(=x^2+2xy+y^2+2xz+2yz+z^2\)
\(=x^2+y^2+z^2+2xy+2yz+2zx=VP\)
Chúc bạn học tốt.

1)5(x^2-1)+x(1-5x)= x-2
<=>5x2-5+x-5x2=x-2
<=>-5+x=x-2
<=>x-x=-2+5
<=>0x=3(vô lí)
vậy ko tìm được x

thực hiện nhân đa thức với đa thức ở vế trái xog rút gọn là nó = vế pải
1/ Biến đổi vế trái , ta có :
(x-y)(x+y)= x2+xy - xy-y2= x2-y2
=> (x-y) (x+y) =x2-y2
2/ Biến đổi vế trái , ta có :
(x-y) (x2+xy+y2)= x3+x2y+xy2-x2y-xy2-y3
= (x2y-x2y)+(xy2-xy2)+x3-y3=x3-y3
=> (x-y) (x2+xy+y2) =x3-y3
3/ / Biến đổi vế trái , ta có :
(x+y) (x2-xy+y2) =x3-x2y+xy2+x2y-xy2+y3
(-x2y+x2y) + ( xy2-xy2) + x3+y3= x3+y3

a) \(x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)
\(\Leftrightarrow2x^2+2y^2\ge\left(x+y\right)^2\Leftrightarrow x^2+y^2\ge2xy\)
\(\Leftrightarrow x^2-2xy+y^2\ge0\Leftrightarrow\left(x-y\right)^2\ge0\left(đúng\right)\)
b) \(x^3+y^3\ge\dfrac{\left(x+y\right)^3}{4}\)
\(\Leftrightarrow4x^3+4y^3\ge\left(x+y\right)^3\Leftrightarrow3x^3+3y^3\ge3x^2y+3xy^2\)
\(\Leftrightarrow3x^2\left(x-y\right)-3y^2\left(x-y\right)\ge0\)
\(\Leftrightarrow3\left(x-y\right)\left(x^2-y^2\right)\ge0\Leftrightarrow3\left(x-y\right)^2\left(x+y\right)\ge0\left(đúng\right)\)
a: Ta có: \(x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)
\(\Leftrightarrow2x^2+2y^2-x^2-2xy-y^2\ge0\)
\(\Leftrightarrow x^2-2xy+y^2\ge0\)
\(\Leftrightarrow\left(x-y\right)^2\ge0\)(luôn đúng)

a)(x-y)(x^2+xy+y^2)+xy(x-y)
=(x-y)(x^2+2xy+y^2)
=(x-y)(x+y)^2
=> Đt trên Đ
b) CM tương tự nha

Câu 1:
a) Ta có: \(VT=x^4-y^4\)
\(=\left(x^2-y^2\right)\left(x^2+y^2\right)\)
\(=\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)\)
\(=\left(x-y\right)\left(x^3+xy^2+x^2y+y^3\right)\)=VP(đpcm)
c) Ta có: \(VT=a\left(b+1\right)+b\left(a+1\right)\)
\(=ab+a+ab+b\)
\(=a+b+2ab\)(1)
Thay ab=1 vào biểu thức (1), ta được:
a+b+2(*)
Ta có: VP=(a+1)(b+1)=ab+a+b+1(2)
Thay ab=1 vào biểu thức (2), ta được:
1+a+b+1=a+b+2(**)
Từ (*) và (**) ta được VT=VP(đpcm)
Câu 2:
Ta có: \(\left(x-3\right)\left(x+x^2\right)+2\left(x-5\right)\left(x+1\right)-x^3=12\)
\(\Leftrightarrow x^2+x^3-3x-3x^2+2\left(x^2+x-5x-5\right)-x^3=12\)
\(\Leftrightarrow x^3-2x^2-3x+2x^2-8x-10-x^3-12=0\)
\(\Leftrightarrow-11x-22=0\)
\(\Leftrightarrow-11x=22\)
hay x=-2
Vậy: x=-2

a) \(N=\left(x-5\right)\left(x+2\right)+3\left(x-2\right)\left(x+2\right)-\left(3x-\dfrac{1}{2}x^2\right)+5x^2\)
\(=x^2+2x-5x-10+3x^2-12-3x+\dfrac{1}{2}x^2+5x^2\)
\(=\dfrac{19}{2}x^2-6x-22\)
Vậy biểu thức trên phụ thuộc vào biến x.
b) \(\left(y-1\right)\left(y^2+y+1\right)=y^3-1\)
Giải:
VT = \(\left(y-1\right)\left(y^2+y+1\right)\)
\(=y^3+y^2+y-y^2-y-1\)
\(=y^3-1\)
Vậy \(\left(y-1\right)\left(y^2+y+1\right)=y^3-1\).
Giải:
a) \(N=\left(x-5\right)\left(x+2\right)+3\left(x-2\right)\left(x+2\right)-\left(3x-\dfrac{1}{2}x^2\right)+5x^2\)
\(\Leftrightarrow N=x^2-3x-10+3\left(x^2-4\right)-3x+\dfrac{1}{2}x^2+5x^2\)
\(\Leftrightarrow N=x^2-3x-10+3x^2-12x-3x+\dfrac{1}{2}x^2+5x^2\)
\(\Leftrightarrow N=-10-18x+\dfrac{19}{2}x^2\)
Vậy biểu thức trên phụ thuộc vào biễn x
b) \(\left(y-1\right)\left(y^2+y+1\right)\)
\(=y^3-y^2+y^2-y+y-1\)
\(=y^3-\left(y^2-y^2\right)-\left(y-y\right)-1\)
\(=y^3-1\)
Vậy ...

Ta có: \(\left(x-y\right)^3+4y\left(2x^2+y^2\right)\)
\(=x^3-3x^2y+3xy^2-y^3+8x^2y+4y^3\)
\(=x^3+5x^2y+3xy^2+3y^3\)
\(=x^3+3x^2y+3xy^2+y^3+2x^2y+2y^3\)
\(=\left(x+y\right)^3+2y\left(x^2+y^2\right)\)
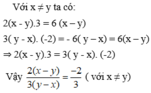
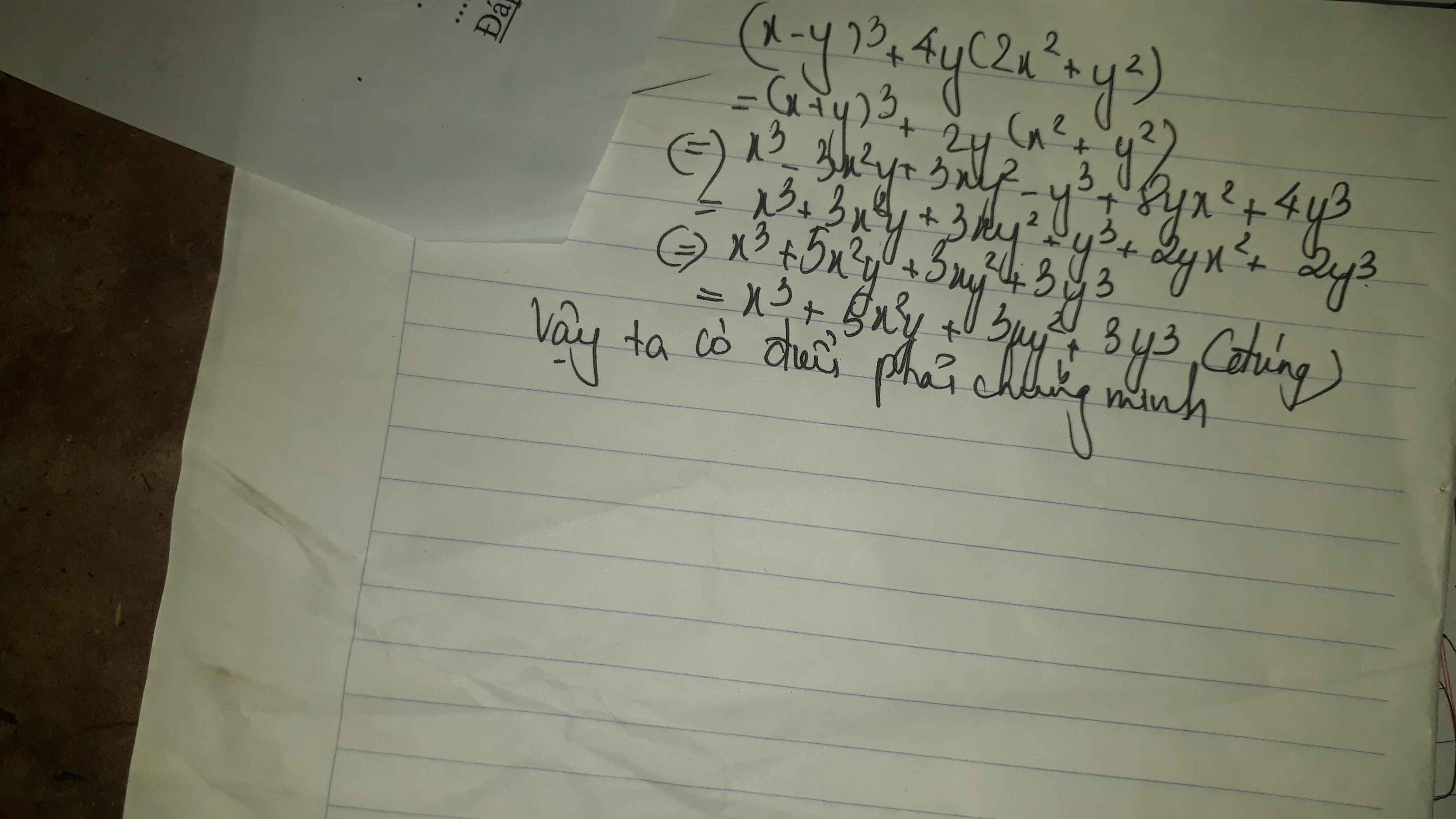
Ta có
Vế trái bằng vế phải nên đẳng thức được chứng minh.