Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Leftrightarrow x+10^0=-90^0+k360^0\)
\(\Leftrightarrow x=-100^0+k360^0\)

Lời giải:
$\sin (x+30^0)=\frac{-1}{2}=\sin (-30^0)$
\(\Rightarrow \left[\begin{matrix} x+30^0=-30^0+360^0k\\ x+30^0=210^0+360^0k\end{matrix}\right.\) với $k$ nguyên
\(\Leftrightarrow \left[\begin{matrix} x=-60^0+360^0k(1)\\ x=180^0+360^0k(2)\end{matrix}\right.\)
Với $(1): $0^0< -60^0+360^0k< 3600^0$
$\Leftrightarrow \frac{1}{6}< k< 10$
Mà $k$ nguyên nên $k=1;2;3;...;9$. Bạn thay các giá trị này vô $(1)$ để tìm $x$
Với $(2): $0^0< 180^0+360^0k< 3600^0$
$\Leftrightarrow \frac{-1}{2}< k< 9,5$. Mà $k$ nguyên nên $k=0,1,2,..,9$. Bạn thay các giá trị này vô $(2)$ để tìm $x$

Đường tròn (C) có tâm I(2; -4), bán kính R= 3
Đường tròn (C’) có tâm J( 3; -3) và bán kính R’ = 3
Vì R= R’ nên tồn tại phép đối xứng tâm: biến đường tròn (C) thành (C’).
Khi đó; tâm đối xứng K là trung điểm IJ.
x K = 2 + 3 2 = 5 2 y K = ( − 4 ) + ( − 3 ) 2 = − 7 2
⇒ K 5 2 ; - 7 2
Đáp án D

Lời giải:
$\sin (2x+1)=\frac{-1}{2}$
$\Rightarrow 2x+1=\frac{-\pi}{6}+2k\pi$ hoặc $2x+1=\frac{7}{6}\pi +2k\pi$ với $k$ nguyên
Với $2x+1=\frac{-\pi}{6}+2k\pi$
Do $x\in (0;\pi)$ nên $k=1$
$x=\frac{11}{12}\pi -\frac{1}{2}$
Với $2x+1=\frac{7\pi}{6}+2k\pi$
Do $x\in (0;\pi)$ nên $k=0$
$\Rightarrow x=\frac{7}{12}\pi -\frac{1}{2}$


Phép vị tự tâm H (1; -3) tỉ số k = 1/2, biến tâm I(2; 3) của (C) thành I’(x; y)
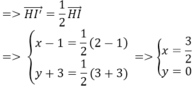
biến bán kính R = 4√2 thành R' = 2√2 ⇒ phương trình (C’) là:
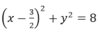
Đáp án D
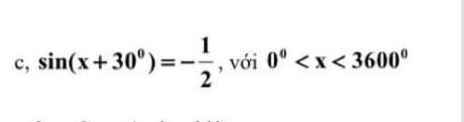
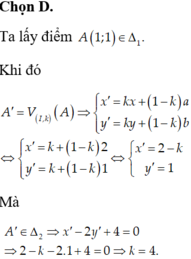
1: cos(3x-45 độ)=0
=>3x-45 độ=90 độ+k*180 độ
=>3x=135 độ+k*180 độ
=>x=45 độ+k*60 độ
=45 độ-120 độ+(k+2)*60 độ
=-75 độ+z*60 độ
=>Chọn B
2;
tan(x-15 độ)=1
=>x-15 độ=45 độ+k*180 độ
=>x=60 độ+k*180 độ
=>Chọn C
3: 2*cos(4x-20 độ)=0
=>cos(4x-20 độ)=0
=>4x-20 độ=90 độ+k*180 độ
=>4x=110 độ+k*180 độ
=>x=27,5 độ+k*45 độ
=>Chọn C