Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x^{2010}+y^{2010}=x^{2011}+y^{2011}=x^{2012}+y^{2012}\)
\(\Leftrightarrow x^{2010}+x^{2012}-2x^{2011}+y^{2010}+y^{2012}-2y^{2011}=0\)
\(\Leftrightarrow x^{2010}\left(x^2-2x+1\right)+y^{2010}\left(y^2-2y+1\right)=0\)
\(\Leftrightarrow x^{2010}\left(x-1\right)^2+y^{2010}\left(y-1\right)^2=0\)
\(x^{2010};y^{2010}>0\Leftrightarrow x=y=1.\Rightarrow x^{2016}+y^{2016}=2\)
\(x^{2010}+y^{2010}=x^{2011}+y^{2011}=x^{2012}+y^{2012}\)
\(\Leftrightarrow x^{2010}+x^{2012}-2x^{2011}+y^{2010}+y^{2012}-2y^{2011}=0\)
\(\Leftrightarrow x^{2010}\left(x^2-2x+1\right)+y^{2010}\left(y^2-2y+1\right)=0\)
\(\Leftrightarrow x^{2010}\left(x-1\right)^2+y^{2010}\left(y-1\right)^2=0\)
\(x^{2010};y^{2010}>0\Leftrightarrow x=y=1.\Rightarrow x^{2016}+y^{2016}=2\)
...................................................................................................................

Sửa đề: \(P=x^{2008}+y^{2009}+z^{2010}\)
Ta có: x+y+z=1
nên \(\left(x+y+z\right)^3=1\)
\(\Leftrightarrow x^3+y^3+z^3+3\left(x+y\right)\left(y+z\right)\left(x+z\right)=1\)
\(\Leftrightarrow3\left(x+y\right)\left(y+z\right)\left(z+x\right)+1=1\)
\(\Leftrightarrow3\left(x+y\right)\left(y+z\right)\left(x+z\right)=0\)
mà 3>0
nên \(\left(x+y\right)\left(y+z\right)\left(x+z\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+y=0\\y+z=0\\x+z=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-y\\y=-z\\x=-z\end{matrix}\right.\)
Thay x=-y vào biểu thức \(x+y+z=1\), ta được:
\(-y+y+z=1\)
hay z=1
Thay x=-y và z=1 vào biểu thức \(x^2+y^2+z^2=1\), ta được:
\(\left(-y\right)^2+y^2+1=1\)
\(\Leftrightarrow y^2+y^2=0\)
\(\Leftrightarrow2y^2=0\)
hay y=0
Vì x=-y
và y=0
nên x=0
Thay x=0; y=0 và z=1 vào biểu thức \(P=x^{2008}+y^{2009}+z^{2010}\), ta được:
\(P=0^{2008}+0^{2009}+1^{2010}=1\)
Vậy: P=1
nma ở trên cm y=-z mà. Nếu ở thay y=0 và z=1 vào thì nghĩa là 0 = -1 hả

\(A=x^4+y^4\)
\(=\left(x^4+2x^2y^2+y^4\right)-2x^2y^2\)
\(=\left(x^2+y^2\right)^2-2\left(xy\right)^2\) (*)
Thay xy=5 và x2+y2=18 vào (*), ta có
\(A=18^2-2.5^2\)
\(=324-50\)
\(=274\)
Vậy A=274

cho mk hỏi chút sao chỗ từ (1), (2) lại suy ra đc 1= x+y-xy vậy?
Bài ni t mần cho phát chán nó rồi:))
Ta có:\(x^{2012}+y^{2012}=\left(x^{2011}+y^{2011}\right)\left(a+b\right)-ab\left(a^{2010}+b^{2010}\right)\left(1\right)\)
Mặt khác:\(x^{100}+y^{100}=x^{101}+y^{101}=x^{102}+y^{102}\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow1=x+y-xy\)
\(\Rightarrow\left(x-1\right)\left(y-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=1\Rightarrow1+y^{2010}=1+y^{2011}=1+y^{2012}\Rightarrow y=1\\y=1\Rightarrow x^{2010}+1=x^{2011}+1=x^{2012}+1\Rightarrow x=1\end{cases}}\)vì \(x;y\) là các số dương
Thay vào ta được:\(A=1^{2020}+1^{2020}=2\)

Ta có:
\(\frac{x^4}{a}+\frac{y^4}{b}\ge\frac{\left(x^2+y^2\right)^2}{a+b}=\frac{1}{a+b}\)
Dấu = xảy ra khi .... Làm tiếp nhé
ta có: \(\frac{x^4}{a}+\frac{y^4}{b}=\frac{1}{a+b}\)=> \(\frac{bx^4+ay^4}{ab}=\frac{\left(x^2+y^2\right)^2}{a+b}\) (vì x^2 +y^2 =1)
=>\(abx^4+b^2x^4+aby^4+a^2y^4\) = \(ab\left(x^4+2x^2y^2+y^4\right)\)
=>\(abx^4+b^2x^4+aby^4+a^2y^4\) = \(abx^4+2abx^2y^2+aby^4\)
=> \(b^2x^4-2abx^2y^2+a^2y^4=0\)
=>\(\left(bx^2-ay^2\right)^2=0\)=>\(bx^2=ay^2\Rightarrow\frac{x^2}{a}=\frac{y^2}{b}=\frac{x^2+y^2}{a+b}=\frac{1}{a+b}\)
=> \(\frac{x^{2012}}{a^{1006}}=\frac{1}{\left(a+b\right)^{1006}}\) và \(\frac{y^{2012}}{b^{1006}}=\frac{1}{\left(a+b\right)^{1006}}\)
=>\(\frac{x^{2012}}{a^{1006}}+\frac{y^{2012}}{b^{1006}}=\frac{2}{\left(a+b\right)^{1006}}\)

Độ dài cạnh của tam giác bằng 7 cm và 13 cm
Mà tam giác này cân
=> Cạnh còn lại của tam giác là 7 cm ( Dựa vào bất đẳng thức tam giác 0
Chu ci tam giác là :
7 + 13 + 7 = 27 ( cm )
Vậy chu vi tam giác đó là ; 27 cm
TH1:Cạnh đáy bằng 7 cm
Chu vi của hình tam cân đó là :
13x2+7=33(cm)
TH2:Cạnh đáy bằng 13 cm
Chu vi của hình tam giác cân đó là :
7x2+13=27(cm)
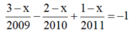
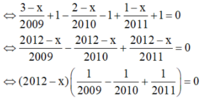
+ \(\left(x^{2011}+y^{2011}\right)\left(x+y\right)\)
\(=x^{2012}+y^{2012}+xy\left(x^{2010}+y^{2010}\right)\)
\(=\left(x^{2011}+y^{2011}\right)+xy\left(x^{2011}+y^{2011}\right)\)
\(=\left(xy+1\right)\left(x^{2011}+y^{2011}\right)\)
+ Vì x, y dương nên \(x^{2011}+y^{2011}>0\)
=> x + y = xy + 1
=> x + y - xy - 1 = 0
=> ( y - 1 ) - x( y - 1 ) = 0
=> ( 1 - x ) ( y - 1 ) = 0
\(\Rightarrow\left[{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
+ x = 1 => \(1+y^{2010}=1+y^{2011}=1+y^{2012}\)
\(\Rightarrow y^{2010}=y^{2011}\) \(\Rightarrow y^{2010}-y^{2011}=0\)
\(\Rightarrow y^{2010}\left(1-y\right)=0\)
\(\Rightarrow y=1\left(doy>0\right)\)
+ Tương tự nếu y = 1 ta cùng tìm được x = 1
Do đó : A = 2
Lời giải khác:
Ta có:
\(x^{2011}+y^{2011}=x^{2010}+y^{2010}\)
\(\Rightarrow x^{2011}-x^{2010}+y^{2011}-y^{2010}=0\)
\(\Leftrightarrow x^{2010}(x-1)+y^{2010}(y-1)=0(1)\)
Và: \(x^{2011}+y^{2011}=x^{2012}+y^{2012}\)
\(\Rightarrow x^{2012}-x^{2011}+y^{2012}-y^{2011}=0\)
\(\Leftrightarrow x^{2011}(x-1)+y^{2011}(y-1)=0(2)\)
Lấy (2)-(1) ta có:
\(x^{2011}(x-1)-x^{2010}(x-1)+y^{2011}(y-1)-y^{2010}(y-1)=0\)
\(\Leftrightarrow x^{2010}(x-1)^2+y^{2010}(y-1)^2=0\)
Dễ thấy \(x^{2010}(x-1)^2\geq 0; y^{2010}(y-1)^2\geq 0, \forall x,y>0\)
Do đó để tổng của chúng bằng $0$ thì \(x^{2010}(x-1)^2=y^{2010}(y-1)^2=0\)
Mà $x,y$ đều dương nên $x=y=1$
Khi đó ta dễ tính ra $A=2$