Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác AOC và tam giác BOC có:
AO = BO (gt)
AOC = BOC (OC là tia phân giác của AOB)
OC là cạnh chung
=> Tam giác AOC = Tam giác BOC (c.g.c)
OA = OB (gt)
=> Tam giác OAB cân tại O
mà OI là tia phân giác của AOB
=> OI là đường trung trực của tam giác OAB
=> I là trung điểm của AB
OI _I_ AB
Ta có hình vẽ:
Vì Oz là phân giác của xOy nên \(xOz=zOy=\frac{xOy}{2}\)
Xét Δ AOC và Δ BOC có:
OA = OB (gt)
góc AOC = góc BOC (chứng minh trên)
OC là cạnh chung
Do đó, Δ AOC = Δ BOC (c.g.c) (đpcm)
Vì Δ AOC = Δ BOC nên AC = BC (2 cạnh tương ứng)
góc ACO = góc BCO (2 góc tương ứng)
Xét Δ AIC và Δ BIC có:
AC = BC (chứng minh trên)
góc ACI = BCI (chứng minh trên)
CI là cạnh chung
Do đó, Δ AIC = Δ BIC (c.g.c)
=> AI = IB (2 cạnh tương ứng)
=> I là trung điểm của đoạn AB (đpcm)
Vì Δ AIC = Δ BIC nên góc AIC = BIC (2 góc tương ứng)
Lại có: AIC + BIC = 180o (kề bù)
Do đó, góc AIC = góc BIC = 90o
=> \(AB\perp OC\left(đpcm\right)\)

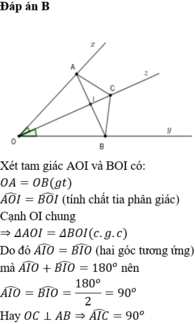
a) Xét ΔOAI và ΔOBI có
OA=OB(gt)
\(\widehat{AOI}=\widehat{BOI}\)(OI là tia phân giác của \(\widehat{AOB}\))
OI chung
Do đó: ΔOAI=ΔOBI(c-g-c)
b) Xét ΔOHA và ΔOHB có
OA=OB(gt)
\(\widehat{AOH}=\widehat{BOH}\)(OH là tia phân giác của \(\widehat{AOB}\))
OH chungDo đó: ΔOHA=ΔOHB(c-g-c)
nên AH=BH(hai cạnh tương ứng)
mà A,H,B thẳng hàng(gt)
nên H là trung điểm của AB(đpcm)
a) Xét tam giác OAI và tam giác OBI:
^AOI = ^BOI (Oz là tia phân giác của góc xOy)
OA = OB (gt)
OI chung
=> Tam giác OAI = Tam giác OBI (c - g - c)
b) Xét tam giác AOB có: OA = OB (gt)
=> Tam giác AOB cân tại A
Lại có: OH là đường phân giác của góc xOy (H \(\in Oz\))
=> OH là đường trung tuyến (TC các đường trong tam giác cân)
=> H là trung điểm của AB

a: Xét ΔOAI và ΔOBI có
OA=OB
\(\widehat{AOI}=\widehat{BOI}\)
OI chung
Do đó: ΔOAI=ΔOBI
1: Xét ΔAOC và ΔBOC
OC chung
\(\widehat{AOC}=\widehat{BOC}\)
OA=OB
Do đó: ΔAOC=ΔBOC
1)Xét ΔAOCvàΔOBC có:
OC:cạnh chung
OB=OA(GT)
gócBOC=gócAOC(vì Oz là p/g của góc xOy)
Do đó Δ AOC= Δ OBC(c.g.c)
2)a)Xét Δ OIB và Δ OIA có:
OI:cạnh chung
OB=OA(GT)
góc BOC= góc AOC(vì Oz là p/g của góc xOy)
Suy ra ΔOIB =Δ OIA(c.g.c)
⇒BI=IA⇒I là trung điểm của AB
b)vì ΔOIB=ΔOIA(câu a) nên góc OIB= góc OIA(2 góc tương ứng)
Mà góc OIB+góc OIA=180 nên góc OIB= góc OIA=180/2=90
⇒OI⊥AB hay OC⊥AB