
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(A-B=2x^2y+xy+4-7xy^2+8xy^2+xy-4x^2y-2\)
\(=-2x^2y+2xy+2+xy^2\)
bậc 3
\(A+B=2x^2y+xy+4-7xy^2-8xy^2-xy+4x^2y+2\)
\(=6x^2y-15xy^2+6\)
bậc 3


\(x-y=2\Rightarrow x=2+y\)
a) Thay x = 2+y vào P:
\(P=\left(2+y\right)y+4\)
\(=2y+y^2+4\)
\(=2\left(y^2+y+4\right)\)
\(=2\left(y^2+\dfrac{1}{2}y+\dfrac{1}{2}y+4\right)\)
\(=2\left[\left(y+\dfrac{1}{2}\right)^2+\dfrac{15}{4}\right]\)
\(=2\left(y+\dfrac{1}{2}\right)^2+\dfrac{15}{2}\)
Vì \(2\left(y+\dfrac{1}{2}\right)^2\ge0\Rightarrow2\left(y+\dfrac{1}{2}\right)^2+\dfrac{15}{2}\ge\dfrac{15}{2}\)
Dấu "=" xảy ra khi \(\left(y+\dfrac{1}{2}\right)^2=0\)
\(\Rightarrow y=\dfrac{-1}{2}\)
Khi đó: \(x=\dfrac{-1}{2}+2=\dfrac{3}{2}\)
Vậy ...
Ta có \(x-y=2\Rightarrow x=y+2\)
a,Thay x=y+2 vào P ta được:
\(P=y\left(y+2\right)+4=y^2+2y+4=\left(y+1\right)^2+3\ge3\)
Vậy GTNN của P = 3 khi y=-1 và x=1
b,Cũng thay như thế ta được
\(Q=\left(y+2\right)^2+y^2-y\left(y+2\right)=y^2+2y+4\)
Vậy GTNN của Q=3 khi y=-1 và x=1

2,
M + N = 3xyz - 3x2 + 5xy - 1 + 5x2 + xyz - 5xy + 3 - y
= -3x2 + 5x2 + 3xyz + xyz + 5xy - 5xy - y - 1 + 3
= 2x2 + 4xyz - y +2.
M - N = (3xyz - 3x2 + 5xy - 1) - (5x2 + xyz - 5xy + 3 - y)
= 3xyz - 3x2 + 5xy - 1 - 5x2 - xyz + 5xy - 3 + y
= -3x2 - 5x2 + 3xyz - xyz + 5xy + 5xy + y - 1 - 3
= -8x2 + 2xyz + 10xy + y - 4.
N - M = (5x2 + xyz - 5xy + 3 - y) - (3xyz - 3x2 + 5xy - 1)
= 5x2 + xyz - 5xy + 3 - y - 3xyz + 3x2 - 5xy + 1
= 5x2 + 3x2 + xyz - 3xyz - 5xy - 5xy - y + 3 + 1
= 8x2 - 2xyz - 10xy - y + 4.
3,
a) P + (x2 – 2y2) = x2 – y2 + 3y2 – 1
P = (x2 – y2 + 3y2 – 1) - (x2 – 2y2)
P = x2 – y2 + 3y2 – 1 - x2 + 2y2
P = x2 – x2 – y2 + 3y2 + 2y2 – 1
P = 4y2 – 1.
Vậy P = 4y2 – 1.
b) Q – (5x2 – xyz) = xy + 2x2 – 3xyz + 5
Q = (xy + 2x2 – 3xyz + 5) + (5x2 – xyz)
Q = xy + 2x2 – 3xyz + 5 + 5x2 – xyz
Q = 7x2 – 4xyz + xy + 5
Vậy Q = 7x2 – 4xyz + xy + 5.
4,
a, Thu gọn : x2+2xy-3x3+2y3+3x3-y3
= x2+2xy+(-3x3+3x3)+2y3-y3
=x2+2xy+2y3-y3
Thay x=5,y=4 vào đa thức x2+2xy+2y3-y3 Ta có:
52 + 2.5.4 + 43 = 25 + 40 + 64 = 129.
Vậy giá trị của đa thức x2+2xy+2y3-y3 tại x=5,y=4 là 129
b,
Thay x = -1; y = -1 vào biểu thức xy-x2y2+x4y4-x6y6+x8y8 Ta Có
M = (-1)(-1) - (-1)2.(-1)2 + (-1)4. (-1)4-(-1)6.(-1)6 + (-1)8.(-1)8
= 1 -1 + 1 - 1+ 1 = 1.
Vậy giá trị của biểu thức xy-x2y2+x4y4-x6y6+x8y8 tại x=-1, y=-1 là 1
5,
a, C=A+B
C = x2 – 2y + xy + 1 + x2 + y - x2y2 - 1
C = 2x2 – y + xy - x2y2
b) C + A = B => C = B - A
C = (x2 + y - x2y2 - 1) - (x2 – 2y + xy + 1)
C = x2 + y - x2y2 - 1 - x2 + 2y - xy - 1
C = - x2y2 - xy + 3y - 2.

Lời giải:
Thay \(x=y+2\) ta có:
a)
\(P=xy+4=(y+2)y+4=y^2+2y+4=(y+1)^2+3\)
\(\geq 0+3=3\)
Vậy GTNN của $P$ là $3$ khi \(y+1=0\Leftrightarrow y=-1; x=1\)
b)
\(Q=x^2+y^2-xy=(y+2)^2+y^2-(y+2)y\)
\(=y^2+2y+4=(y+1)^2+3\geq 0+3=3\)
Vậy GTNN của $Q$ là $3$ khi \(y+1=0\Leftrightarrow y=-1; x=1\)
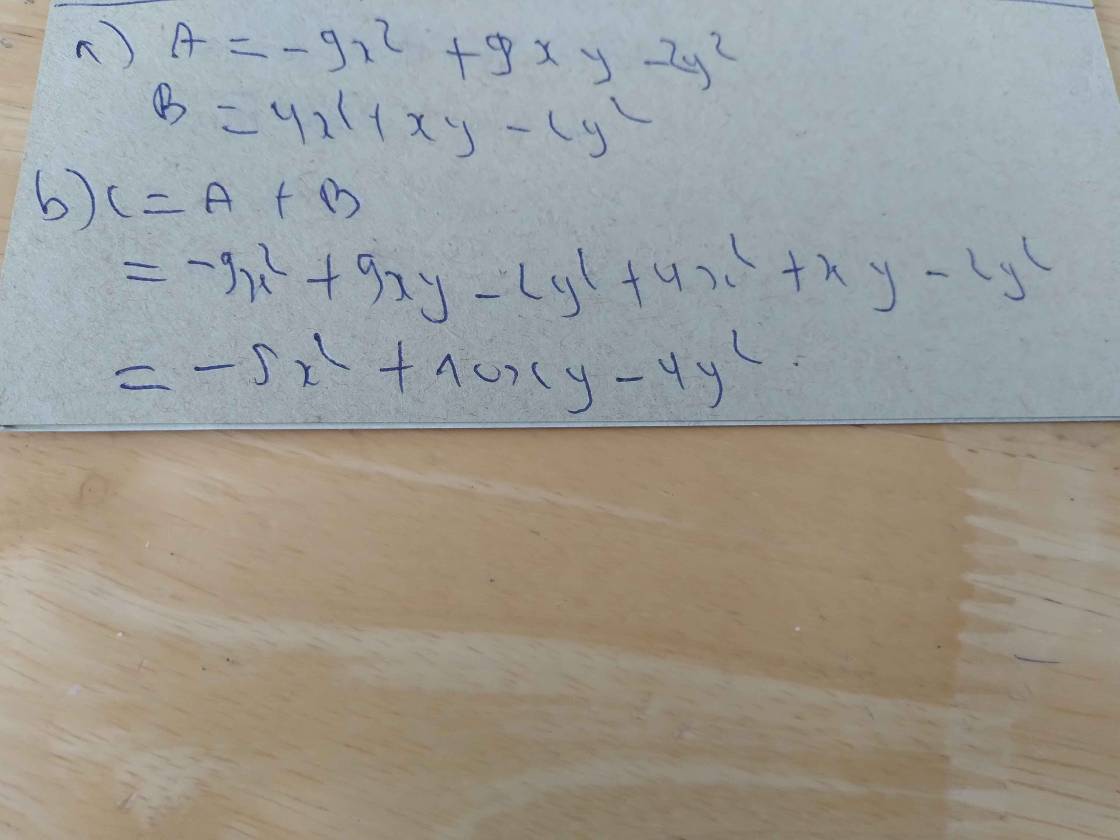
Lamborghini Aventardo VSJ chứ
Giải được một bài thôi,bạn thông cảm!
b)Ta có: \(Q_{min}=x^2+y^2-xy=x^2-xy+y^2=\left(x-y\right)^2=2^2=4\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}x=2\\y=0\end{cases}}\)