Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Từ giả thiết, suy ra
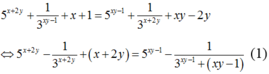
Xét hàm số f ( t ) = 5 t - 1 3 t + t trên ℝ .
Đạo hàm f ' ( t ) = 5 t . ln 5 - ln 3 3 t + 1 > 0 , ∀ t ∈ ℝ ⇒ hàm số f ( t ) luôn đồng biến trên ℝ .
Suy ra
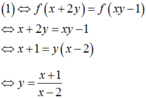
Do y > 0 nên x + 1 x - 2 > 0 ⇔ [ x > 2 x < - 1 . Mà x > 0 nên x > 2 .
Từ đó T = x + y = x + x + 1 x - 2 . Xét hàm số g ( x ) = x + x + 1 x - 2 trên 2 ; + ∞ .
Đạo hàm
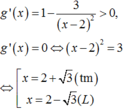
Lập bảng biến thiên của hàm số trên 2 ; + ∞ , ta thấy min g ( x ) = g ( 2 + 3 ) = 3 + 2 3 .
Vậy T m i n = 3 + 2 3 khi x = 2 + 3 và x = 1 + 3 .

Từ giả thiết ta suy ra
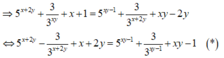
Xét hàm số f ( t ) = 5 t - 1 3 t + t với t ∈ ℝ , f ' ( t ) = 5 t . ln 5 + 3 - t . ln 3 + 1 > 0 ; ∀ t ∈ ℝ
Suy ra y= f( t) là hàm số đồng biến trên R mà từ ( * ) suy ra
f (x+ 2y) =f( xy-1) hay x+ 2y= xy-1
![]()
với x>0 suy ra y>1.
Khi đó
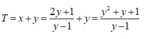
Xét hàm số
f ( y ) = y 2 + y + 1 y - 1 t r ê n 1 ; + ∞ f ' y = y 2 - 2 y - 2 y - 1 2 = 0 ⇔ y = ± 1 + 3 f 1 + 3 = 3 + 2 3 ; lim y → 1 f ( y ) = lim y → + ∞ f ( y ) = + ∞
Do đó, giá trị nhỏ nhất của hàm số là 3 + 2 3 .
Vậy kết quả là 3 + 2 3
Chọn B.

\(P=xy-3\left(x+y\right)+9\)
Đặt \(x+y=a\Rightarrow1< a\le\sqrt{2}\)
\(a^2=x^2+y^2+2xy=1+2xy\Rightarrow xy=\frac{a^2-1}{2}\)
\(P=\frac{a^2-1}{2}-3a+9\Rightarrow2P=a^2-6a+17\)
\(2P=a^2-6a-2+6\sqrt{2}+19-6\sqrt{2}\)
\(2P=\left(a+\sqrt{2}\right)\left(a-\sqrt{2}\right)-6\left(a-\sqrt{2}\right)+19-6\sqrt{2}\)
\(2P=\left(\sqrt{2}-a\right)\left(6-\sqrt{2}-a\right)+19-6\sqrt{2}\ge19-6\sqrt{2}\)
\(\Rightarrow P\ge\frac{19-6\sqrt{2}}{2}\)
Dấu "=" xảy ra khi \(a=\sqrt{2}\) hay \(x=y=\frac{\sqrt{2}}{2}\)

Bạn ơi có thể hướng dẫn chi tiết giúp mình không? cám ơn nhiều ạ

\(\left(xy-1\right)2^{2xy-1}=\left(x^2+y\right)2^{x^2+y}\)
\(\Leftrightarrow\left(xy-1\right)2^{2\left(xy-1\right)+1}=\left(x^2+y\right)2^{x^2+y}\)
\(\Leftrightarrow2\left(xy-1\right)2^{2\left(xy-1\right)}=\left(x^2+y\right)2^{x^2+y}\)
Do vế phải luôn dương \(\Rightarrow VT>0\Rightarrow xy-1>0\) (1)
Xét hàm \(f\left(t\right)=t.2^t\) với \(t>0\Rightarrow f'\left(t\right)=2^t+t.2^t.ln2>0\)
\(\Rightarrow f\left(t\right)\) đồng biến \(\Rightarrow f\left(t_1\right)=f\left(t_2\right)\Leftrightarrow t_1=t_2\)
\(\Rightarrow2\left(xy-1\right)=x^2+y\Rightarrow2xy-y=x^2+2\) (thay \(x=\dfrac{1}{2}\) thấy ko phải nghiệm)
\(\Rightarrow y=\dfrac{x^2+2}{2x-1}\) (2)
Thay (2) vào (1): \(xy-1>0\Rightarrow x.\left(\dfrac{x^2+2}{2x-1}\right)-1>0\Rightarrow\dfrac{x^3+2x}{2x-1}-1>0\)
\(\Rightarrow\dfrac{x^3+1}{2x-1}>0\Rightarrow2x-1>0\) (do \(x>0\Rightarrow x^3+1>0\))
Vậy \(y=\dfrac{x^2+2}{2x-1}=\dfrac{1}{2}x+\dfrac{1}{4}+\dfrac{9}{4\left(2x-1\right)}=\dfrac{2x-1}{4}+\dfrac{9}{4\left(2x-1\right)}+\dfrac{1}{2}\)
\(\Rightarrow y\ge2\sqrt{\dfrac{\left(2x-1\right)}{4}.\dfrac{9}{4\left(2x-1\right)}}+\dfrac{1}{2}=2\)
\(\Rightarrow y_{min}=2\) khi \(\dfrac{2x-1}{4}=\dfrac{9}{4\left(2x-1\right)}\Rightarrow x=2\)
Đáp án B

Đặt \(x+y=t,t\in\left[-2;2\right]\)
Biến đổi được \(P=-2t^3+6t\)
Xét \(f\left(t\right)=-2t^3+6t\) trên \(\left[-2;2\right]\)
Lập bảng biến thiên
Ta có \(P_{Max}=4\) khi t=1
\(P_{Min}=-4\) khi t= -1

\(\Leftrightarrow log_{\frac{1}{3}}xy\le log_{\frac{1}{3}}\left(x+y^2\right)\)
\(\Rightarrow xy\ge x+y^2\) (do \(\frac{1}{3}< 1\))
\(\Rightarrow x\left(y-1\right)\ge y^2\) (\(y-1>0\) do
Nếu \(y\le1\Rightarrow\left\{{}\begin{matrix}VT\le0\\VP>0\end{matrix}\right.\) (vô lý)
\(\Rightarrow y>1\Rightarrow x\ge\frac{y^2}{y-1}\)
\(\Rightarrow P=2x+3y\ge\frac{2y^2}{y-1}+3y=5y+2+\frac{2}{y-1}\)
\(\Rightarrow P\ge5\left(y-1\right)+\frac{2}{y-1}+7\ge2\sqrt{\frac{10\left(y-1\right)}{y-1}}+7=7+2\sqrt{10}\)
\(P_{min}=7+2\sqrt{10}\) khi \(\left\{{}\begin{matrix}y=1+\frac{\sqrt{10}}{5}\\x=\frac{y^2}{y-1}=...\end{matrix}\right.\)

\(x^2+\left(y-3\right)x+y^2-4y+4=0\)
\(\Delta=\left(y-3\right)^2-4\left(y^2-4y+4\right)\ge0\)
\(\Leftrightarrow-3y^2+10y-7\ge0\Rightarrow1\le y\le\frac{7}{3}\)
\(y^2+\left(x-4\right)y+x^2-3x+4=0\)
\(\Delta=\left(x-4\right)^2-4\left(x^2-3x+4\right)\ge0\)
\(\Leftrightarrow-3x^2+4x\ge0\Rightarrow0\le x\le\frac{4}{3}\)
Mặt khác ta có:
\(P=3x^3-3y^3+20x^2+5y^2+39x+2\left(-x^2-y^2+4y+3x-4\right)\)
\(P=\left(3x^3+18x^2+45x\right)+\left(-3y^3+3y^2+8y-8\right)=f\left(x\right)+f\left(y\right)\)
Xét hàm \(f\left(x\right)=3x^3+18x^2+45x\) trên \(\left[0;\frac{4}{3}\right]\)
\(f'\left(x\right)=9x^2+36x+45>0\Rightarrow f\left(x\right)\) đồng biến
\(\Rightarrow f\left(x\right)\le f\left(\frac{4}{3}\right)=\frac{892}{9}\)
Xét \(f\left(y\right)=-3y^3+3y^2+8y-8\) trên \(\left[1;\frac{7}{3}\right]\)
\(f'\left(y\right)=-9y^2+6y+8=0\Rightarrow y=\frac{4}{3}\)
\(f\left(1\right)=0\) ; \(f\left(\frac{4}{3}\right)=\frac{8}{9}\) ; \(f\left(\frac{7}{3}\right)=-\frac{100}{9}\)
\(\Rightarrow f\left(y\right)_{max}=f\left(\frac{4}{3}\right)=\frac{8}{9}\Rightarrow f\left(y\right)\le\frac{8}{9}\)
\(\Rightarrow P\le\frac{892}{9}+\frac{8}{9}=100\)