Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đầu bài ta có: log 2x+ log2y=log4(x+y) hay 2 log 2(xy) =log2(x+y)
Suy ra x+y=(xy) 2
Đặt u= x+ y; v= xy ta có điều kiện u2-4v≥0; u>0; v>0 .
Mà ![]()
Ta có
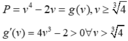
nên minP=
2
4
3
khi 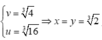
Chọn A.

Đáp án C
Tọa độ giao điểm của hai đồ thị là nghiệm của phương trình
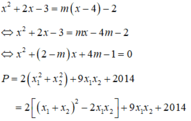
![]()
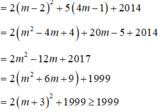
Dấu “=” xảy ra khi và chỉ khi m = -3

Do \(x^2+y^2=1\), đặt \(\left\{{}\begin{matrix}x=sina\\y=cosa\end{matrix}\right.\)
\(P=\left(3-sina\right)\left(3-cosa\right)=9-3\left(sina+cosa\right)+sina.cosa\)
Đặt \(sina+cosa=t\Rightarrow t\in\left[-\sqrt{2};\sqrt{2}\right]\)
\(t^2=1+2sina.cosa\Rightarrow sina.cosa=\dfrac{t^2-1}{2}\)
\(P=9-3t+\dfrac{t^2-1}{2}=\dfrac{1}{2}t^2-3t+\dfrac{17}{2}\)
Xét hàm \(f\left(t\right)=\dfrac{1}{2}t^2-3t+\dfrac{17}{2}\) trên \(\left[-\sqrt{2};\sqrt{2}\right]\)
\(f'\left(t\right)=t-3=0\Rightarrow t=3\notin\left[-\sqrt{2};\sqrt{2}\right]\)
\(f\left(-\sqrt{2}\right)=\dfrac{19+6\sqrt{2}}{2}\) ; \(f\left(\sqrt{2}\right)=\dfrac{19-6\sqrt{2}}{2}\)
\(\Rightarrow P_{min}=f\left(\sqrt{2}\right)=\dfrac{19-6\sqrt{2}}{2}\) khi \(t=\sqrt{2}\)

a. Đề bài em ghi sai thì phải
Vì:
\(x+y=2\left(\sqrt{x-3}+\sqrt{y-3}\right)\)
\(\Leftrightarrow\left(x-3-2\sqrt{x-3}+1\right)+\left(y-3-2\sqrt{y-3}+1\right)+4=0\)
\(\Leftrightarrow\left(\sqrt{x-3}-1\right)^2+\left(\sqrt{y-3}-1\right)^2+4=0\) (vô lý)
b.
Xét hàm \(f\left(x\right)=x^3+ax^2+bx+c\)
Hàm đã cho là hàm đa thức nên liên tục trên mọi khoảng trên R
Hàm bậc 3 nên có tối đa 3 nghiệm
\(f\left(-2\right)=-8+4a-2b+c>0\)
\(f\left(2\right)=8+4a+2b+c< 0\)
\(\Rightarrow f\left(-2\right).f\left(2\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc (-2;2)
\(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=x^3\left(1+\dfrac{a}{x}+\dfrac{b}{x^2}+\dfrac{c}{x^3}\right)=+\infty.\left(1+0+0+0\right)=+\infty\)
\(\Rightarrow\) Luôn tồn tại 1 số thực dương n đủ lớn sao cho \(f\left(n\right)>0\)
\(\Rightarrow f\left(2\right).f\left(n\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(2;n\right)\) hay \(\left(2;+\infty\right)\)
Tương tự \(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=-\infty\Rightarrow f\left(-2\right).f\left(m\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(-\infty;-2\right)\)
\(\Rightarrow f\left(x\right)\) có đúng 3 nghiệm pb \(\Rightarrow\) hàm cắt Ox tại 3 điểm pb

Đáp án C.
Ta có: GT
<=> 5x+2y + x + 2y – 3–x–2y = 5xy–1 – 31–xy + xy – 1.
X é t h à m s ố f t = 5 t + t - 3 - t
⇒ f t = 5 t ln 5 + 1 + 3 - t ln 3 > 0 ∀ t ∈ ℝ
Do đó hàm số đồng biến trên ℝ suy ra
f(x+2y) = f(xy – 1) <=> x+ 2y = xy – 1
⇔ x = 2 y + 1 y - 1 ⇒ T = 2 y + 1 y - 1 + y .
Do x > 0 => y > 1.
Ta có:
T = 2 + y + 3 y - 1 = 3 + y - 1 + 3 y - 1 ≥ 3 + 2 3 .

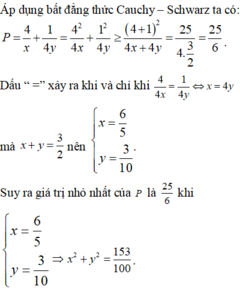

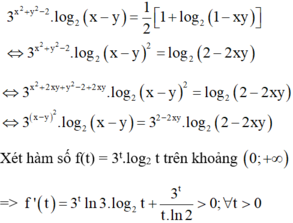

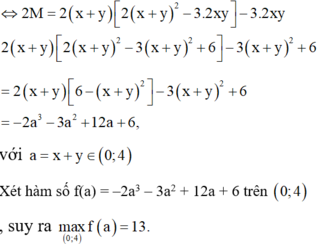
Chọn A.
Theo đầu bài ta có : 2log2xy = log2(x + y) hay x + y = (xy) 2
Đặt u = x + y và v = xy ta có điều kiện u2 - 4v ≥ 0 ; u > 0; v > 0.
Mà u = v2 nên v4 - 4v ≥ 0 suy ra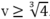
Ta có P = v4 - 2v = g(v) với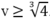
Đạo hàm g’(v) = 4v3-2 > 0 với mọi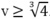
nên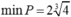 khi
khi