Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho điểm M(-4;2) và vecto v =(3;-1). Tìm điểm N biết M là ảnh của N qua phép tịnh tiến theo vecto v.

\(T_{\overrightarrow{v}}\left(N\right)=M\Rightarrow\overrightarrow{NM}=\overrightarrow{v}\)
\(\Rightarrow\left\{{}\begin{matrix}x_N+3=-4\\y_N-1=2\end{matrix}\right.\) \(\Rightarrow N\left(-7;3\right)\)

a) M(-1;1) đối xứng qua trục Oy ta được N(-1;1).
Gọi M'(x;y) là ảnh của N(-1;1) qua phép tịnh tiến theo vectơ v → = ( 2 ; 0 )
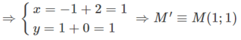
b) Gọi P(x;y) là ảnh của M(1;1) qua phép tịnh tiến theo v → = ( 2 ; 0 )
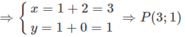
P(3;1) đối xứng qua trục Oy ta được M"(-3;1)

Tọa độ E là:
\(\left\{{}\begin{matrix}x=6-2=4\\y=-3-\left(-5\right)=-3+5=2\end{matrix}\right.\)
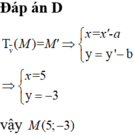
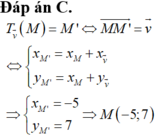

Sử dụng biểu thức tọa độ của phép tịnh tiến
Đáp án A