Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho đường tròn (o) có đường kính AB=15 . Dây CD vuông góc với AB, CD=12, tính diện tích tứ giác ABCD

Đúng òi
Gọi I là gd của AB và CD
=>SABC=1/2.CI.AB
=>SABD=1/2.DI.AB
=>SACBD=1/2 CI.AB+1/2.DI.AB=1/2DI.AB+1/2.DI.AB=DI.AB=6.15=45 ko bik đúng ko

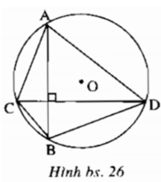
Ta có AB ≤ 4cm, CD ≤ 4cm. Do AB ⊥ CD nên S A C B D = 1/2AB.CD ≤ 1/2.4.4 = 8 ( c m 2 )
Giá trị lớn nhất của S A C B D bằng 8 c m 2 khi AB và CD đều là đường kính của đường tròn.

Ủa sao lại 2 tam giác hay 2 tứ giác nhỉ? BE chia hình thang thành 1 tam giác và 1 tứ giác chứ?
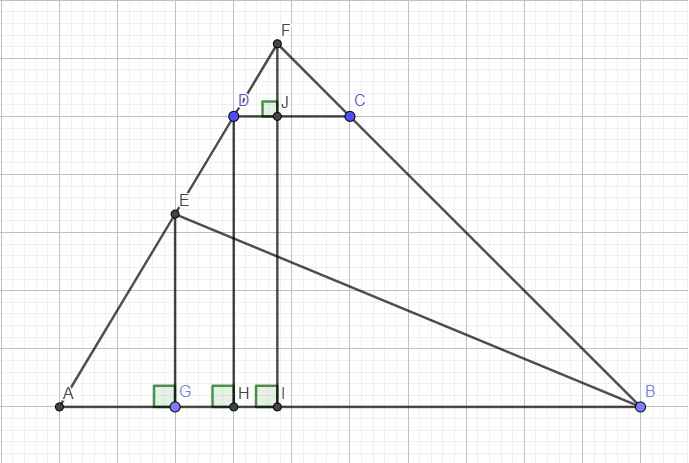
Hướng dẫn là em kéo dài AD và BC cắt nhau tại F. Sử dụng định lý Talet
\(\dfrac{DF}{AF}=\dfrac{CD}{AB}=\dfrac{1}{5}\) \(\Rightarrow\dfrac{DF}{AD}=\dfrac{1}{4}\) ; \(\dfrac{AD}{AF}=\dfrac{4}{5}\)
\(EA=3DE\Rightarrow\dfrac{AE}{AD}=\dfrac{3}{4}\Rightarrow\dfrac{AE}{AF}=\dfrac{3}{5}\)
Từ E, D, F hạ vuông góc xuống AB tại G, H, I, FI cắt CD tại J
Talet: \(FJ=\dfrac{1}{5}FI\) ; \(\dfrac{DH}{FI}=\dfrac{AD}{AF}=\dfrac{4}{5}\Rightarrow DH=\dfrac{4}{5}FI\) ; \(\dfrac{EG}{FI}=\dfrac{AE}{AF}=\dfrac{3}{5}\Rightarrow EG=\dfrac{3}{5}FI\)
\(S_{ABF}=\dfrac{1}{2}FI.AB\)
\(S_{DCF}=\dfrac{1}{2}FJ.DC=\dfrac{1}{2}.\dfrac{1}{5}FI.\dfrac{1}{5}AB=\dfrac{1}{25}\left(\dfrac{1}{2}FI.AB\right)=\dfrac{1}{25}S_{ABF}\)
\(\Rightarrow S_{ABCD}=S_{ABF}-S_{CDF}=\dfrac{24}{25}S_{ABF}\)
\(S_{ABE}=\dfrac{1}{2}EG.AB=\dfrac{1}{2}.\dfrac{3}{5}FI.AB=\dfrac{3}{5}S_{ABF}\)
\(\Rightarrow S_{BCDE}=S_{ABCD}-S_{ABE}=\dfrac{24}{25}S_{ABF}-\dfrac{3}{5}S_{ABF}=\dfrac{9}{25}S_{ABF}\)
\(\Rightarrow\dfrac{S_{ABE}}{S_{BCDE}}=\dfrac{\dfrac{3}{5}S_{ABF}}{\dfrac{9}{25}S_{ABF}}=\dfrac{5}{3}\)
Chi tiết phân giác góc B thừa, ko cần sử dụng

Bạn xem hình vẽ ở đây nhé: https://i.imgur.com/sh8KysD.png
Gọi CD giao AB tại O, Đặt OD=a, OA=b.
Xét tam giác OAD vuông tại O ta có
a^2 + b^2 =25
Xét tam giác OBC vuông tại O ta có
(a+8^2 )+ (b+2^2=13^2
Từ đó tính được a=84/17 hoặc a=4. Loại a=84/17vì với a=84/17 thì b<0
Với a=4 suy ra b=3. Khi đó SABCD=SOBC-SOAD=24
Bạn xem hình vẽ ở đây nhé: https://i.imgur.com/sh8KysD.png
Gọi CD giao AB tại O, Đặt OD=a, OA=b.
Xét tam giác OAD vuông tại O ta có \(a^2+b^2=25\)
Xét tam giác OBC vuông tại O ta có \(\left(a+8\right)^2+\left(b+2\right)^2=13^2\)
Từ đó tính được a \(=\frac{87}{17}\)hoặc a = 4. Loại a = \(\frac{87}{17}\)vì với a = \(\frac{87}{17}\) thì \(b< 0\)
Với a = 4 suy ra b = 3. Khi đó \(^SABCD=^SOBC-^SOAD=24\)