Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:

a) Xét trên mp(BCD): NP cắt CD tại I
I thuộc NP suy ra I nằm trên mp(MNP)
Suy ra giao điểm của CD và mp(MNP) là I
b) Ta có I, M đều thuộc mp(ACD) suy ra IM nằm trên mp(ACD)
I, M đều thuộc mp(MNP) suy ra IM nằm trên mp(MNP)
Do đó, IM là giao tuyến của 2 mp(ACD) và mp(MNP) hay EM là giao tuyến của 2 mp(ACD) và mp(MNP).

a) Ta có: MP cắt BC tại E mà BC thuộc (BCD)
Nên: E là giao điểm của đường thẳng MP với mặt phẳng (BCD).
b) Ta có: EN cắt CD tại Q mà EN thuộc (MNP)
Nên: Q là giao điểm của đường thẳng CD với mặt phẳng (MNP).
c) Ta có: P thuộc (MNP) và (ACD)
Q thuộc (MNP) và (ACD)
Nên PQ là giao tuyến của mặt phẳng (ACD) với mặt phẳng (MNP).
d) △ACN có: \(\dfrac{AP}{AC}=\dfrac{AG}{AN}=\dfrac{2}{3}\)
Suy ra: PG // CN
Do đó: △PIG đồng dạng với △NIC
Do đó: C, I, G thẳng hàng.

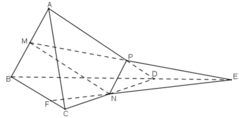
a) Trong mp(ABD): MP không song song với BD nên MP ∩ BD = E.
E ∈ MP ⇒ E ∈ (PMN)
E ∈ BD ⇒ E ∈ (BCD)
⇒ E ∈ (PMN) ∩ (BCD)
Dễ dàng nhận thấy N ∈ (PMN) ∩ (BCD)
⇒ EN = (PMN) ∩ (BCD)
b) Trong mp(BCD) : gọi giao điểm EN và BC là F.
F ∈ EN, mà EN ⊂ (PMN) ⇒ F ∈ (PMN)
⇒ F = (PMN) ∩ BC.

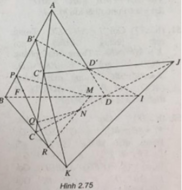
a) Chú ý rằng I, J, K thẳng hàng vì chúng cùng thuộc giao tuyến của hai mặt phẳng (CBD) và (C'B'D')
b) 4. Vì 4 điểm không đồng phẳng sẽ tạo nên 1 tứ diện => có 4 mặt



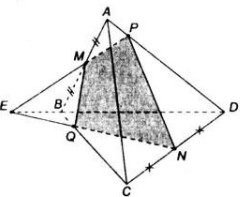
Tham khảo:
a) Tam giác ABC có: MP cắt AC tại E
Mà MP thuộc (MNP)
Nên E là giao điểm của AC và (MNP)
Tam giác ABD có: MN cắt BD tại F
Mà MN thuộc (MNP)
Nên F là giao điểm của BD và (MNP)
b) Ta có: P thuộc BC
F thuộc BD
Suy ra PF thuộc (BCD)
Do đó PF và CD cùng thuộc (BCD)
Nên PF và CD cắt nhau tại một điểm (1)
Ta có: N thuộc AD
E thuộc AC
Suy ra NE thuộc (ACD)
Do đó NE và CD cắt nhau tại một điểm (2)
Từ (1) và (2) suy ra: NE, PE, CD cùng đi qua một điểm