Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

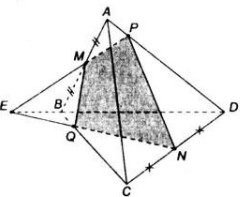
a) Trong mp(ABD): MP không song song với BD nên MP ∩ BD = E.
E ∈ MP ⇒ E ∈ (PMN)
E ∈ BD ⇒ E ∈ (BCD)
⇒ E ∈ (PMN) ∩ (BCD)
Dễ dàng nhận thấy N ∈ (PMN) ∩ (BCD)
⇒ EN = (PMN) ∩ (BCD)
b) Trong mp(BCD) : gọi giao điểm EN và BC là F.
F ∈ EN, mà EN ⊂ (PMN) ⇒ F ∈ (PMN)
⇒ F = (PMN) ∩ BC.

a.
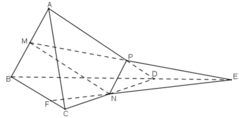
Trong mp (SAB), nối MN kéo dài cắt AB tại E
\(\Rightarrow\left\{{}\begin{matrix}E\in\left(MNP\right)\\E\in\left(ABCD\right)\end{matrix}\right.\)
Mặt khác theo giả thiết \(\left\{{}\begin{matrix}P\in\left(ABCD\right)\\P\in\left(MNP\right)\end{matrix}\right.\)
\(\Rightarrow EP=\left(MNP\right)\cap\left(ABCD\right)\)
b.
Theo giả thiết: \(\left\{{}\begin{matrix}M\in\left(MNP\right)\\M\in SA\Rightarrow M\in\left(SAD\right)\end{matrix}\right.\)
Trong mp (ABCD), nối EP kéo dài cắt AD tại F
\(\Rightarrow\left\{{}\begin{matrix}F\in\left(MNP\right)\\F\in\left(SAD\right)\end{matrix}\right.\)
\(\Rightarrow MF=\left(MNP\right)\cap\left(ABCD\right)\)
c.
Trong mp (SBC), nối NP kéo dài cắt SC tại H
\(\Rightarrow\left\{{}\begin{matrix}H\in\left(MNP\right)\\H\in\left(SCD\right)\end{matrix}\right.\)
Gọi giao điểm của EP và CD tại K
\(\Rightarrow HK=\left(MNP\right)\cap\left(SCD\right)\)

Đáp án A
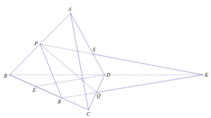
Xét (BCD) có: RQ ∩ BD = K
⇒ K ∈ (ABD)
Xét (ABD) có: PK ∩ AD = S
Gọi E là trung điểm BR
⇒ R là trung điểm đoạn EC
Mà Q là trung điểm CD
⇒ RQ là đường trung bình tam giác DEC
⇒ RQ // DE ⇒ RK // DE
Xét tam giác BRK có: RK // DE và E là trung điểm BR
⇒ D là trung điểm BK
Xét tam giác ABK có: AD là đường trung tuyến cạnh BK
và KP là đường trung tuyến cạnh AB
PK ∩ AD = S
⇒ S là trọng tâm tam giác ABK
⇒ S A S D = 2

a) Ta có: MP cắt BC tại E mà BC thuộc (BCD)
Nên: E là giao điểm của đường thẳng MP với mặt phẳng (BCD).
b) Ta có: EN cắt CD tại Q mà EN thuộc (MNP)
Nên: Q là giao điểm của đường thẳng CD với mặt phẳng (MNP).
c) Ta có: P thuộc (MNP) và (ACD)
Q thuộc (MNP) và (ACD)
Nên PQ là giao tuyến của mặt phẳng (ACD) với mặt phẳng (MNP).
d) △ACN có: \(\dfrac{AP}{AC}=\dfrac{AG}{AN}=\dfrac{2}{3}\)
Suy ra: PG // CN
Do đó: △PIG đồng dạng với △NIC
Do đó: C, I, G thẳng hàng.

Đáp án C

Trong (ABC) có EF ∩ AC = I
⇒ I ∈ (ACD)
Xét (ACD) có: IG ∩ AD = H
⇒ EFGH là thiết diện cần tìm