NT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ND
1
31 tháng 10 2017
Cho tỉ lệ thức: \(\frac{a}{b}=\frac{c}{d}\). Chứng minh rằng:
\(\frac{a^3}{c^3}=\frac{\left(2a-b\right)^3+b^3}{\left(2c-d\right)^3+d^3}\)
BÀI LÀM:
Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk;c=dk\)
Ta có: \(\frac{\left(2a-b\right)^3+b^3}{\left(2c-d\right)^3+d^3}=\frac{\left(2bk-b\right)^3+b^3}{\left(2dk-d\right)^3+d^3}=\frac{b^3.\left(2k-1\right)^3+b^3}{d^3.\left(2k-1\right)^3+d^3}=\frac{b^3.\left[\left(2k-1\right)^3+1\right]}{d^3.\left[\left(2k-1\right)^3+1\right]}=\frac{b^3}{d^3}\left(1\right)\)
Vì \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a^3}{b^3}=\frac{c^3}{d^3}\left(2\right)\)
Từ (1) và (2) => \(\frac{a^3}{c^3}=\frac{\left(2a-b\right)^3+b^3}{\left(2c-d\right)^3+d^3}\left(đpcm\right)\)
25 tháng 6 2022
Đặt a/b=c/d=k
=>a=bk; c=dk
\(\left(\dfrac{a+b}{c+d}\right)^3=\left(\dfrac{bk+b}{dk+d}\right)^3=\dfrac{b^3}{d^3}\)
\(\dfrac{a^3+b^3}{c^3+d^3}=\dfrac{b^3k^3+b^3}{d^3k^3+d^3}=\dfrac{b^3}{d^3}\)
Do đó: \(\left(\dfrac{a+b}{c+d}\right)^3=\dfrac{a^3+b^3}{c^3+d^3}\)
23 tháng 10 2016
Ta có: \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\Rightarrow\frac{a^3}{c^3}=\frac{b^3}{d^3}\)
Áp dụng tính chất của dãy tỉ số = nhau ta có:
\(\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}\Rightarrow\frac{a^3}{c^3}=\frac{b^3}{d^3}=\left(\frac{a+b}{c+d}\right)^3\left(1\right)\)
\(\frac{a^3}{c^3}=\frac{b^3}{d^3}=\frac{a^3+b^3}{c^3+d^3}\left(2\right)\)
Từ (1); (2) \(\Rightarrow\left(\frac{a+b}{c+d}\right)^3=\frac{a^3+b^3}{c^3+d^3}\left(đpcm\right)\)
VA
1
MN
8 tháng 1 2016
Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk;c=dk\)
\(\left(\frac{a+b}{c+d}\right)^3=\left(\frac{bk+b}{dk+d}\right)^3=\left(\frac{b\left(k+1\right)}{d\left(k+1\right)}\right)^3=\left(\frac{b}{d}\right)^3\left(1\right)\)
\(\frac{a^3+b^3}{c^3+d^3}=\frac{\left(bk\right)^3+b^3}{\left(dk\right)^3+d^3}=\frac{b^3k^3+b^3}{d^3k^3+d^3}=\frac{b^3\left(k^3+1\right)}{d^3\left(k^3+1\right)}=\frac{b^3}{d^3}=\left(\frac{b}{d}\right)^3\left(2\right)\)
Từ (1) & (2)=>\(\left(\frac{a+b}{c+d}\right)^3=\frac{a^3+b^3}{c^3+d^3}\)
12 tháng 1
1: Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
=>\(a=b\cdot k;c=d\cdot k\)
\(\dfrac{a}{a+b}=\dfrac{bk}{bk+b}=\dfrac{bk}{b\left(k+1\right)}=\dfrac{k}{k+1}\)
\(\dfrac{c}{c+d}=\dfrac{dk}{dk+d}=\dfrac{dk}{d\left(k+1\right)}=\dfrac{k}{k+1}\)
Do đó: \(\dfrac{a}{a+b}=\dfrac{c}{c+d}\)
2: \(\dfrac{2a+b}{a-2b}=\dfrac{2\cdot bk+b}{bk-2b}=\dfrac{b\left(2k+1\right)}{b\left(k-2\right)}=\dfrac{2k+1}{k-2}\)
\(\dfrac{2c+d}{c-2d}=\dfrac{2dk+d}{dk-2d}=\dfrac{d\left(2k+1\right)}{d\left(k-2\right)}=\dfrac{2k+1}{k-2}\)
Do đó: \(\dfrac{2a+b}{a-2b}=\dfrac{2c+d}{c-2d}\)
3: \(\dfrac{a+b}{a-b}=\dfrac{bk+b}{bk-b}=\dfrac{b\left(k+1\right)}{b\cdot\left(k-1\right)}=\dfrac{k+1}{k-1}\)
\(\dfrac{c+d}{c-d}=\dfrac{dk+d}{dk-d}=\dfrac{d\left(k+1\right)}{d\left(k-1\right)}=\dfrac{k+1}{k-1}\)
Do đó: \(\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
4: \(\dfrac{5a+3b}{5c+3d}=\dfrac{5\cdot bk+3b}{5dk+3d}=\dfrac{b\left(5k+3\right)}{d\left(5k+3\right)}=\dfrac{b}{d}\)
\(\dfrac{5a-3b}{5c-3d}=\dfrac{5\cdot bk-3b}{5\cdot dk-3d}=\dfrac{b\left(5k-3\right)}{d\left(5k-3\right)}=\dfrac{b}{d}\)
Do đó: \(\dfrac{5a+3b}{5c+3d}=\dfrac{5a-3b}{5c-3d}\)
25 tháng 9 2019
Mỗi tỉ số đã cho bằng \(\frac{a+b+c}{b+c+d}\). Tích của ba tỉ số đã cho bằng \(\frac{a^3+b^3+c^3}{b^3+c^3+d^3}\).
Mặt khác tích đó cũng bằng : \(\frac{a}{b}\cdot\frac{b}{c}\cdot\frac{c}{d}=\frac{a}{d}\)
Vậy : ...
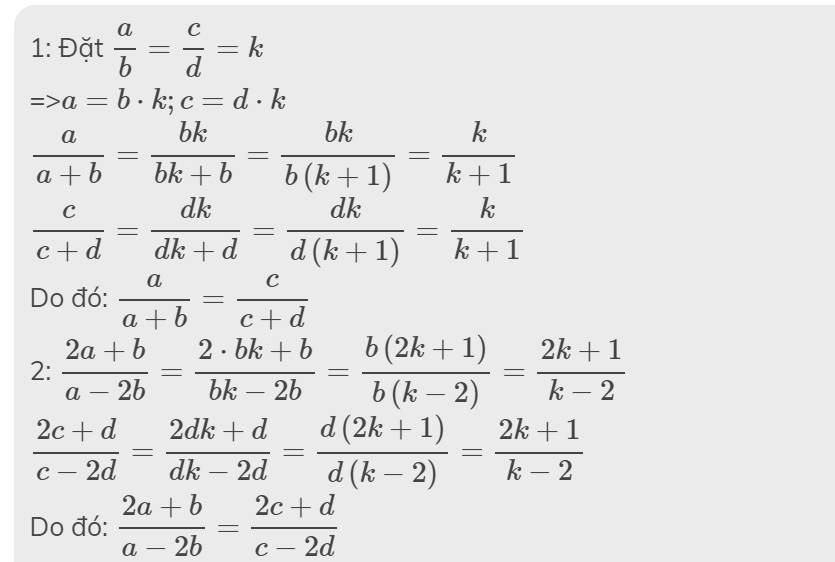
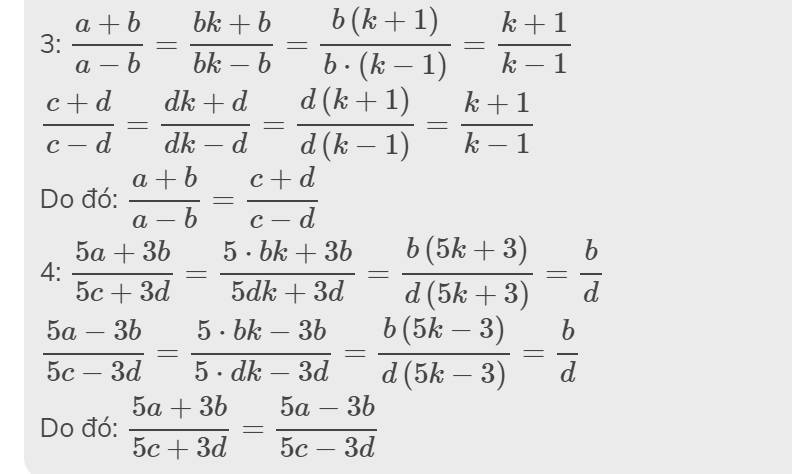
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
=>\(\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có:\(\left(\dfrac{a+b}{c+d}\right)^3=\left(\dfrac{bk+b}{dk+d}\right)^3=\left(\dfrac{b.\left(k+1\right)}{d.\left(k+1\right)}\right)^3=\dfrac{b^3}{d^3}\)(1)
Lại có :\(\dfrac{a^3+b^3}{c^3+d^3}=\dfrac{b^3k^3+b^3}{d^3k^3+d^3}=\dfrac{b^3.\left(k^3+1\right)}{d^3.\left(k^3+1\right)}=\dfrac{b^3}{d^3}\)(2)
Từ (1) và (2) => ĐPCM
Từ a/b=c/d
=>a/c=b/d=a+b/c+d
<=>a^3/c^3=b^3/d^3=(a+b)^3(c+d)^3
=a^3+b^3/c^3+d^3
Vậy
(a+b)^3(c+d)^3=a^3+b^3/c^3+d^3 (đpcm)