Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Do \({A_1}{F_1} = a - c\) và \({A_1}{F_2} = a - c\) nện\({A_1}{F_1} + {A_1}{F_2} = 2a\).Vậy \({A_1}\left( { - a;{\rm{ }}0} \right)\) thuộc elip (E).
Mà A (-1; 0) thuộc trục Ox nên \({A_1}\left( { - a;{\rm{ }}0} \right)\) là giao điểm của elip (E) với trục Ox.
Tương tự, ta chứng minh được \({A_2}\left( {a;{\rm{ }}0} \right)\) là giao điểm của clip (E) với trục Ox.
b) Ta có:\({B_2}{F_2} = \sqrt {{{\left( {c - 0} \right)}^2} + {{\left( {0 - b} \right)}^2}} = \sqrt {{c^2} + {b^2}} = \sqrt {{a^2}} = a\).Vì \({B_2}{F_1} = {B_2}{F_2}\) nên\({B_2}{F_1} + {B_2}{F_2} = a + a = 2a\). Do đó, \({B_2}\left( {0{\rm{ }};{\rm{ }}b} \right)\) thuộc elip (E). Mà \({B_2}\left( {0{\rm{ }};{\rm{ }}b} \right)\)thuộc trục Oy nên \({B_2}\left( {0{\rm{ }};{\rm{ }}b} \right)\)là giao điểm của elip (E) với trục Oy.
Tương tự, ta chứng minh được: \({B_1}\left( {0{\rm{ }};{\rm{ - }}b} \right)\)là giao ddiemr của elip (E) với trục Oy.
Như vậy, elip (E) đi qua bốn điểm \({A_1}\left( { - a;{\rm{ }}0} \right)\)\({A_2}\left( {a{\rm{ }};{\rm{ }}0} \right)\)\({B_1}\left( {0; - {\rm{ }}b} \right)\)\({B_2}\left( {0;{\rm{ }}b} \right)\)

a) Phương trình tổng quát của đường thẳng \({\Delta _1}\) là: \(2\left( {x - 1} \right) + 1\left( {y - 3} \right) = 0 \Leftrightarrow 2x + y - 5 = 0\).
b) Phương trình tham số của đường thẳng \({\Delta _2}\) là:\(\left\{ \begin{array}{l}x = - 2 + 3t\\y = 1 + 2t\end{array} \right.\)
c) Phương trình đường thẳng AB đi qua điểm \(A\left( {1;3} \right)\) nhận \(\overrightarrow {AB} = \left( { - 3; - 2} \right)\) là vectơ chỉ phương nên phương trình tham số của AB là \(\left\{ \begin{array}{l}x = 1 - 3t\\y = 3 - 2t\end{array} \right.\)

a) Phương trình tổng quát của đường thẳng\(\Delta \) đi qua điểm \(A\left( { - 1;{\rm{ }}2} \right)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {3{\rm{ }};{\rm{ }}2} \right).\)là: \(3\left( {x + 1} \right) + 2\left( {y - 2} \right) = 0 \Leftrightarrow 3x + 2y - 1 = 0\)
b) Do \(\Delta \) có vecto chỉ phương là \(\overrightarrow u = \left( { - 2{\rm{ }};{\rm{ 3}}} \right).\)nên vecto pháp tuyến của \(\Delta \) là \(\overrightarrow n = \left( {3{\rm{ }};{\rm{ }}2} \right).\)
Phương trình tổng quát của đường thẳng\(\Delta \) đi qua điểm \(A\left( { - 1;{\rm{ }}2} \right)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {3{\rm{ }};{\rm{ }}2} \right).\)là: \(3\left( {x + 1} \right) + 2\left( {y - 2} \right) = 0 \Leftrightarrow 3x + 2y - 1 = 0\)

Khi M thay đổi, hiệu \(M{F_1} - M{F_2} = \left( {M{F_1} + MA} \right) - \left( {M{F_2} + MA} \right) = AB - l{\rm{ }}\)không đổi.

a) Ta có:
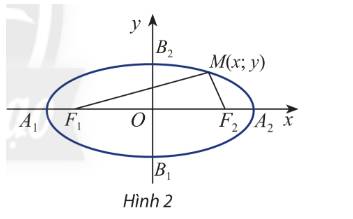
\(\overrightarrow {{F_1}M} = \left( {x + c;y} \right) \Rightarrow {F_1}M = \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} \)
\(\overrightarrow {{F_2}M} = \left( {x - c;y} \right) \Rightarrow {F_2}M = \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} \)
b) Ta có \(M(x;y) \in (E)\) nên \({F_1}M + {F_2}M = 2a \Leftrightarrow \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} + \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} = 2a\)

phương trình (E) có dạng:
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)
Vì (E) đi qua điểm M nên
\(\dfrac{\dfrac{9}{5}}{a^2}+\dfrac{\dfrac{16}{5}}{b^2}=1\)
\(\dfrac{9}{a^2}+\dfrac{16}{b^2}=5\)(1)
Do tam giác \(MF_1F_2\)vuông tại M
Nên M thuộc đường tròn \(x^2+y^2=c^2\)
\(\dfrac{9}{5}+\dfrac{16}{5}=c^2\)
\(5=c^2\)
\(a^2-b^2=5\)
\(a^2=5+b^2\)
Thế vào pt(1)
\(9b^2+16a^2=5a^2b^2\)
\(9b^2+16\left(5+b^2\right)=5b^2\left(5+b^2\right)\)
\(5b^4-80=0\)
\(b^2=\pm4\)
\(\Rightarrow b^2=4\Rightarrow a^2=9\)
\(\left(E\right):\dfrac{x^2}{4}+\dfrac{y^2}{9}=1\)
\(\Rightarrow c=\sqrt{5};e=\dfrac{\sqrt{5}}{2}\)

a) Tọa độ vecto pháp tuyến của \(\Delta \) là:
Tọa độ vecto chỉ phương của \(\Delta \) là:
b) Chọn \(x = 0;x = 1\) ta lần được được 2 điểm A và B thuộc đường thẳng \(\Delta \) là: \(A\left( {0;1} \right),B\left( {1;2} \right)\)

a) Ta có:
\(\overrightarrow {{F_1}M} = \left( {x + c;y} \right) \Rightarrow {F_1}M = \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} \)
\(\overrightarrow {{F_2}M} = \left( {x - c;y} \right) \Rightarrow {F_2}M = \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} \)
b) Ta có \(M(x;y) \in (E)\) nên \(\left| {{F_1}M - {F_2}M} \right| = 2a \Leftrightarrow \left| {\sqrt {{{\left( {x + c} \right)}^2} + {y^2}} - \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} } \right| = 2a\)



a) Phương trình tổng quát của đường thẳng \(A{F_1}{\rm{ }}\)là:\(\frac{x}{{ - 3}} + \frac{y}{4} = 1 \Leftrightarrow 4x - 3y + 12 = 0\).
Phương trình tổng quát của đường thẳng \(A{F_2}{\rm{ }}\)là:\(\frac{x}{3} + \frac{y}{4} = 1 \Leftrightarrow 4x + 3y - 12 = 0\).
b) Giả sử tâm đường tròn là điểm \(I\left( {a;b} \right)\). Ta có: \(IA = I{F_1} = I{F_2} \Leftrightarrow I{A^2} = I{F_1}^2 = I{F_2}^2\)
Vì \(I{A^2} = I{F_1}^2,I{F_1}^2 = I{F_2}^2\) nên: \(\left\{ \begin{array}{l}{a^2} + {\left( {4 - b} \right)^2} = {\left( { - 3 - a} \right)^2} + {b^2}\\{\left( { - 3 - a} \right)^2} + {b^2} = {\left( {3 - a} \right)^2} + {b^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = \frac{7}{8}\end{array} \right.\) .
=> \(I\left( {0;\frac{7}{8}} \right)\) và \(R = IA = \sqrt {{0^2} + {{\left( {\frac{{25}}{8}} \right)}^2}} = \frac{{25}}{8}\)
Vậy phương trình đường tròn ngoại tiếp tam giác \(A{F_1}{F_2}\) là: \({x^2} + {\left( {y - \frac{7}{8}} \right)^2} = {\left( {\frac{{25}}{8}} \right)^2}\)
c) Gọi phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\left( {a > b > 0} \right)\).
Do elip có 2 tiêu điểm \({F_1},{F_2}\) nên \(\sqrt {{a^2} - {b^2}} = c = 3 \Leftrightarrow {a^2} - {b^2} = 9\).
Mặt khác điểm A thuộc elip nên \(\frac{{16}}{{{b^2}}} = 1 \Leftrightarrow b = 4\left( {do{\rm{ }}b > 0} \right)\). Vậy \(a = 5\).
Vậy phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{{5^2}}} + \frac{{{y^2}}}{{{4^2}}} = 1\).