
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


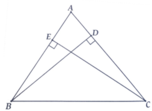
Xét tứ giác BEDC có
góc BEC=góc BDC=90 độ
=>BEDC là tứ giác nội tiếp
=>góc AED=góc ACB
Xét ΔAED và ΔACB có
góc AED=góc ACB
góc A chung
=>ΔAED đồng dạng với ΔACB
=>S AED/S ACB=(AE/AC)^2=(cos60)^2=1/4
=>S AED=1/4*S ACB

Ta có: ∆ABD ~ ∆ACE( g.g) => A D A B = A E A C
=> S A D E S A B C = A E A C 2
Mà trong ∆ACE có cosA = A E A C
=> S A D E S A B C = cos A 2
=> S A D E = S A B C . cos 2 A

c, Xét tam giác ADB vuông tại D có :
cosA = \(\frac{AD}{AB}=\frac{1}{2}\)
Lại có tam giác AED ~ tam giác ACB
\(\Rightarrow\frac{S_{ADE}}{S_{ABC}}=\left(\frac{AD}{AB}\right)^2\Rightarrow\frac{S_{ADE}}{12}=\frac{1}{4}\Rightarrow S_{ADE}=3\)cm2


Xin lỗi bạn nhưng máy mình bị lỗi không vẽ hình được.
c) Tứ giác BEDC là tứ giác nội tiếp (câu a) \(\Rightarrow\widehat{BDE}=\widehat{BCE}\) hay \(\Rightarrow\widehat{BDE}=\widehat{BCQ}\) (1)
Xét (O) có \(\widehat{BCQ}\) và \(\widehat{BPQ}\) là các góc nội tiếp chắn \(\stackrel\frown{BQ}\) \(\Rightarrow\widehat{BCQ}=\widehat{BPQ}\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{BDE}=\widehat{BPQ}\left(=\widehat{BCQ}\right)\)
\(\Rightarrow DE//PQ\) (2 góc đồng vị bằng nhau)
d) Kẻ tia tiếp tuyến Ax của (O) (ở đây mình lấy về phía B chứ còn bạn lấy tia tiếp tuyến này vế phía B hay phía C tùy)
Dễ thấy \(\widehat{BAx}\) và \(\widehat{ACB}\) lần lượt là góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn \(\stackrel\frown{AB}\) \(\Rightarrow\widehat{BAx}=\widehat{ACB}\)
Tứ giác BEDC nội tiếp \(\Rightarrow\widehat{AED}=\widehat{ACB}\) (góc ngoài = góc trong đối)
\(\Rightarrow\widehat{BAx}=\widehat{AED}\left(=\widehat{ACB}\right)\) \(\Rightarrow Ax//DE\) ( 2 góc so le trong bằng nhau)
Vì \(DE//PQ\left(cmt\right)\) \(\Rightarrow Ax//PQ\)\(\left(//DE\right)\)
Mà \(Ax\perp OA\) tại A (do Ax là tiếp tuyến tại A của (O)) \(\Rightarrow OA\perp PQ\) (3)
Xét (O) có OA là 1 phần đường kính và \(OA\perp PQ\left(cmt\right)\)
\(\Rightarrow\) OA đi qua trung điểm của PQ (4)
Từ (3) và (4) \(\Rightarrow\) OA là trung trực của đoạn PQ

a/ E và D cùng nhìn BC dưới 1 góc vuông nên E; D nằm trên đường tròn đường kính BC => B; C; D; E cùng nằm trên đường tròn đường kính BC hay bán kính BC/2
b/
Xét tg vuông ABD
\(\sin\widehat{BAC}=\frac{BD}{AB}=\frac{BD}{8}=\sin60^o=\frac{\sqrt{3}}{2}\Rightarrow BD=4\sqrt{3}\)
Xét tg vuông BCD có
\(BC=\sqrt{BD^2+CD^2}=\sqrt{48+16}=8\Rightarrow\frac{BC}{2}=4\)
TA CÓ \(\Delta ADB\)đồng dạng \(\Delta AEC\)(g-g)
\(\Rightarrow\)\(\frac{AD}{AB}=\frac{AE}{AC}\)
Xét \(\Delta AED\)và \(\Delta ACB\) có :
góc A chung
\(\frac{AD}{AB}=\frac{AE}{AC}\)(CMT)
\(\Rightarrow\Delta AED\infty\Delta ACB\)(c-g-c)
\(\frac{S\Delta AED}{S\Delta ACB}=\left(\frac{AD}{AB}\right)^2\)=\(\frac{3}{4}\)
\(\Rightarrow\frac{AD}{AB}=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\cos A=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\)góc A=60 ĐỘ
cảm ơn bạn nhiều nha!!!!!!!!!!!!!!!!