Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bước 1: Vẽ NP = 7cm
Bước 2: Tại điểm N vẽ cung tròn tâm N bán kính MN = 4cm
Tại điểm P vẽ cung tròn tâm P bán kính MP = 5cm
2 cung tròn này cắt nhau ở đâu thì đó là điểm M
Bước 3: Nối MN, MP ta được tam giác MNP
Cứ làm theo 3 bước trên ta vẽ được tam giác MNP

Đáp án C
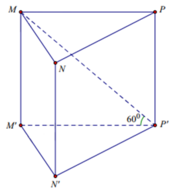
Ta có: M M ' = a tan 60 ∘ = a 3 ; S M N P = 1 2 a 2 sin 60 ∘ = a 2 3 4
Thể tích khối lăng trụ là: V = M M ' . S M N P = a 3 . a 2 2 4 = 3 a 3 4 .

b/
Xét \(\Delta ABD\) và \(\Delta EBC\) có:
\(\widehat{A}=\widehat{E}=90^o\) ( vì \(\Delta ABC\) vuông tại A và \(CE\perp BD\) tại E)
\(\widehat{ABD}=\widehat{EBC}\) ( vì BD là tia phân giác của \(\widehat{ABC}\) )
\(\Rightarrow\Delta ABD~\Delta EBC\left(g.g\right)\)
\(\Rightarrow\dfrac{BD}{BC}=\dfrac{AD}{EC}\) ( 2 cặp cạnh tương ứng tỉ lệ)
\(\Rightarrow BD.EC=BC.AD\)
c/ Vì \(\Delta ABD~\Delta EBC\left(cmt\right)\)
\(\Rightarrow\widehat{ADB}=\widehat{ECB}\)
Mà \(\widehat{ADB}=\widehat{EDC}\) ( 2 góc đối đỉnh)
\(\Rightarrow\widehat{EDC}=\widehat{ECB}\)
Xét \(\Delta ECD\) và \(\Delta EBC\) có:
\(\widehat{E}\) là góc chung
\(\widehat{EDC}=\widehat{ECB}\left(cmt\right)\)
\(\Rightarrow\Delta ECD~\Delta EBC\left(g.g\right)\)
\(\Rightarrow\dfrac{EC}{EB}=\dfrac{CD}{BC}\) ( 2 cặp cạnh tương ứng tỉ lệ)
d/ Xét \(\Delta EBC\) vuông tại E, đường cao EH ứng với cạnh BC
Áp dụng hệ thức lượng trong tam giác vuông ta có:
\(EC^2=CH.CB\) (3)
Vì \(\Delta ECD~\Delta EBC\left(cmt\right)\)
\(\Rightarrow\dfrac{ED}{EC}=\dfrac{EC}{EB}\) ( 2 cặp cạnh tương ứng tỉ lệ)
\(\Rightarrow EC.EC=ED.EB\)
\(\Leftrightarrow EC^2=ED.EB\left(4\right)\)
Từ (3) và (4) \(\Rightarrow CH.CB=ED.EB\)

Mình nói tóm tắt thôi nhé!
a) chứng minh được tam giác ABD = tam giác HBD (cạnh huyền - góc nhọn) => AD = DH (2 cạnh tương ứng)
b) tam giác HDC vuông tại H nên DC là cạnh lớn nhất => DC > DH; mà DH = AH (c/m trên) => DC > AD
c) Mình chưa nghĩ ra![]()
Câu c là tính HC nhé bạn!
c) Tính BC bằng cách dùng định lí pytago trong tam giác ABC, ta có: BC = 10cm
BH + HC = BC = 10cm
BH = AB = 6cm
=> HC = 10 - 6 = 4 cm
Chúc bạn học tốt!![]()

Trong đây có bài y hệt, mong bạn tham khảo:
Cho tam giác ABC vuông tại A , đường phân giác BE.

áp dụng định lí pytago,ta có:
MN2+NP2=62+82=36+84=100(cm)
MP2=102=100(cm)
=> \(\Delta MNP\) vuông tại N
xét 2 tam giác vuông MNE và MKE có:
ME(chung)
\(\widehat{NME}=\widehat{KME}\)
=> \(\Delta MNE=\Delta MKE\left(CH-GN\right)\)
=>EN=NK
a) Xét \(\Delta\)MNP có MN2 + NP2 = MP2 (62 + 82 = 102)
Vậy \(\Delta\)MNP vuông tại N.
b) Xét hai \(\Delta\)MNE và \(\Delta\)MEK có : (1)
\(\widehat{N}=\widehat{K}=90^o\)
ME cạnh chung
\(\widehat{NME}=\widehat{EMK}\left(gt\right)\)
=> Hai tam giác (1) bằng nhau => EN = EK