Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
hay \(\widehat{BAD}=\widehat{BDA}\)
b: Ta có: \(\widehat{CAD}+\widehat{BAD}=90^0\)
\(\widehat{HAD}+\widehat{BDA}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)
nên \(\widehat{CAD}=\widehat{HAD}\)
hay AD là tia phân giác của góc HAC
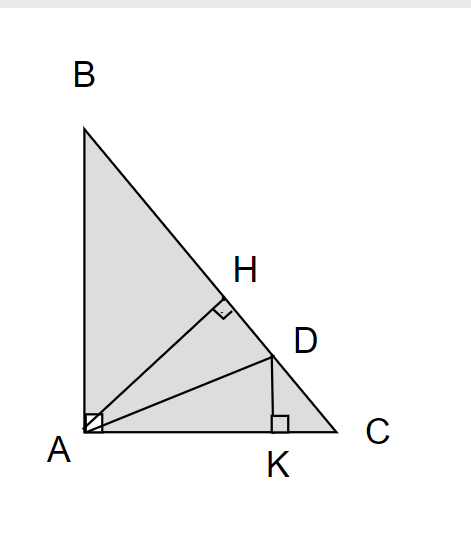
c, Ta có: Góc CAD= góc HAD
hay góc KAD= góc HAD
Xét △ AHD và △AKD có:
AD chung
Góc AHD= góc AKD= 90 độ
Góc KAD= góc HAD
=> △AHD= △AKD (cạnh huyền- góc nhọn)
=> AH= AK (2 cạnh tương ứng)

a) xét tam giác ABD ta có
BA=BA(gt)
-> tam giac ABD cân tại B
-> góc BAD=góc ADB
b) ta có
góc BAD + góc DAC =90 (2 góc kề phụ)
góc ADB + góc HAD=90 ( tam giác AHD vuông tại H)
góc BAD= góc ADB (cma)
-> góc DAC= góc HAD
-> AD là p/g góc HAC
d)
ta có
AB< AH+BH (bất đẳng thức trong tam giac ABH)
AC<AH+HC ( bất đẳng thức trong tam giac AHC)
=> AB+AC < AH+AH+BH+HC
=>AB+AC<2AH+BC

a) Vì BA = BD => tam giác BAD cân tại B => góc BDA = góc DAB
b) Trong tam giác vuông ADH có: góc BDA + DAH = 90o
Mà góc CAD + DAB = CAB = 90o
=> góc BDA + DAH = góc CAD + DAB mà góc BDA = góc DAB
=> góc DAH = CAD => AD là phân giác của HAC
c) Xét tam giác vuông AKD và AHD có: Chung cạnh huyền AD; góc DAH = DAK
=> tam giác AKD = AHD ( cạnh huyền - góc nhọn)
=> AK = AH ( 2 cạnh tương ứng)
dCó DC > KC (tam giác KDC vuông, DC là cạnh huyền)
=> DC + BD+ AK > KC + BD + AK
=> BC +AK > AC + BD
=> AB + AC < BC + AH (vì AK=AH, AB = AD)

a.xét tgiac ABD có AB=BD(gt)
nên theo định nghĩa ta có tgiac ABD cân tại B nên => góc BAD=góc BDA
Bạn tự vẽ hình nha![]()
a.
BA = BD (gt)
=> Tam giác BAD cân tại B
=> BAD = BDA
b.
Tam giác HAD vuông tại H có: HAD + BDA = 90
Ta có: KAD + BAD = 90 (2 góc phụ nhau)
mà BAD = BDA (theo câu a)
=> HAD = KAD
=> AD là tia phân giác của HAK
c.
Xét tam giác HAD vuông tại H và tam giác KAD vuông tại K có:
HAD = KAD (AD là tia phân giác của HAK)
AD là cạnh chung
=> Tam giác HAD = Tam giác KAD (cạnh huyền - góc nhọn)
=> AH = AK (2 cạnh tương ứng)
Chúc bạn học tốt![]()