Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tham khảo
a) Xét tam giác vuông ABE và tam giác vuông HBE (^BAE = ^BHE = 90o)
BE chung
^ABE = ^HBE (BE là phân giác ^ABC)
=> tam giác vuông ABE = tam giác vuông HBE (ch - gn)
b) Ta có: AE = HE (tam giác vuông ABE = tam giác vuông HBE)
=> E thuộc đường trung trực của AH (1)
Ta có: AB = HB (tam giác vuông ABE = tam giác vuông HBE)
=> B thuộc đường trung trực của AH (2)
Từ (1) và (2) => BE là đường trung trực của AH (đpcm)
c) Ta có: ^BEK = ^BEA + ^AEK
^BEC = ^BEH + ^HEC
Mà ^BEA = ^BEH (tam giác vuông ABE = tam giác vuông HBE)
^AEK = ^HEC (2 góc đối đỉnh)
=> ^BEK = ^BEC
Xét tam giác BEK và tam giác BEC:
^BEK = ^BEC (cmt)
^KBE = ^CBE (BE là phân giác ^ABC)
BE chung
=> tam giác BEK = tam giác BEC (g - c - g)
=> EK = EC (cặp cạnh tương ứng)

a) Xét tam giác ABE vuông tại A và ta giác HBE vuông tại H
có: BE là cạnh chung
góc ABE = góc HBE (gt)
\(\Rightarrow\Delta ABE=\Delta HBE\left(ch-gn\right)\)
b) ta có: \(\Delta ABE=\Delta HBE\left(pa\right)\)
=> AE = HE ( 2 cạnh tương ứng)
Xét tam giác AEM vuông tại A và tam giác HEC vuông tại H
có: AE = HE ( cmt)
góc AEM = góc HEC ( đối đỉnh)
\(\Rightarrow\Delta AEM=\Delta HEC\left(cgv-gn\right)\)
=> EM = EC ( 2 cạnh tương ứng)
c) Gọi BE cắt CM tại K
ta có: \(\Delta ABE=\Delta HBE\left(pa\right)\)
=> AB = HB ( 2 cạnh tương ứng) (1)
ta có: \(\Delta AEM=\Delta HEC\) ( chứng minh phần b)
=> AM = HC ( 2 cạnh tương ứng) (2)
Từ (1);(2) => AB + AM = HB + HC
=> BM = BC (*)
Xét tam giác BMH vuông tại H
có: BM > MH ( quan hệ cạnh huyền, cạnh góc vuông) (**)
Từ (*), (**) => BC>MH
mk ko bít kẻ hình trên này, sorry bn nha!

a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
EB chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
=>BA=BH; EA=EH
=>EB là trung trực của AH
c: EA=EH
mà EA<EK
nên EH<EK
d: Xét ΔBHK vuông tại H và ΔBAC vuông tại A có
BH=BA
góc HBK chung
=>ΔBHK=ΔBAC
=>BK=BC
=>ΔBKC cân tại B
mà BE là phân giác
nen BE vuông góc KC

5 )
tự vẽ hình nha bạn
a)
Xét tam giác ABM và tam giác ACM có :
AM cạnh chung
AB = AC (gt)
BM = CM (gt)
suy ra : tam giác ABM = tam giác ACM ( c-c-c)
suy ra : góc BAM = góc CAM ( 2 góc tương ứng )
Hay AM là tia phân giác của góc A
b)
Xét tam giác ABD và tam giác ACD có :
AD cạnh chung
góc BAM = góc CAM ( c/m câu a)
AB = AC (gt)
suy ra tam giác ABD = tam giác ACD ( c-g-c)
suy ra : BD = CD ( 2 cạnh tương ứng)
C) hay tam giác BDC cân tại D

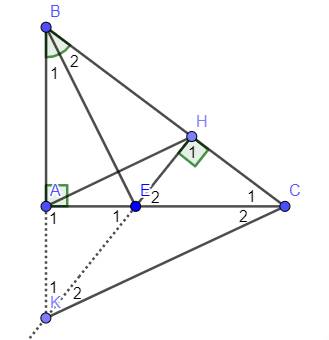
a) Ta có ^BEA = 90 - ^ ABE
^BEH = 90 - ^EBH
mà ^ABE = ^EBH ( do BE là tia phân giác)
=> ^BEA=^BEH
Xét tam giác ABE và Tam giác HBE có
^ABE=^BEH (gt)
BE chung
^BEA=^BEH (cmt)
=> tam giác ABE=Tam giác HBE
b) chỉ cần chứng minh BE là đườn trug tuyến là xog