Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét tam giác AHB và tam giác CAB có:
góc H = góc A = 90 độ
góc B chung
=> tam giác AHB ~ tam giác CAB
=> \(\dfrac{AB}{BC}\)=\(\dfrac{BH}{AB}\)
=> AB2= BH.BC

Ta có :
\(AH^2=AB^2+BH^2\left(1\right)\) (Δ ABH vuông tại H)
\(AH^2=AC^2+CH^2\left(2\right)\) (Δ ACH vuông tại H)
\(\left(1\right),\left(2\right)\Rightarrow AB^2+BH^2=AC^2+CH^2\)
\(\Rightarrow CH^2=AB^2+BH^2-AC^2\)
\(\Rightarrow CH^2=81+676-121=636\)
\(\Rightarrow CH=\sqrt[]{636}=\sqrt[]{4.159}=2\sqrt[]{159}\left(cm\right)\)
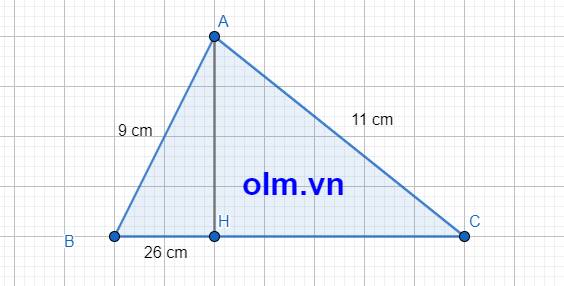
Vì AH là đường cao của tam giác ABC nên AH \(\perp\) BC \(\equiv\) H
⇒ \(\Delta\) AHB \(\perp\) \(\equiv\) H \(\Rightarrow\) AB > BH ⇒ 9 cm > 26 cm vô lý
Em có hai sựa lựa chọn: 1 là em chỉ ra cái sai của cô
2 là em xem lại đề bài của em

\(AH^2=BH.CH=18.32=576\Rightarrow AH=24\left(cm\right)\)
\(AB^2=AH^2+BH^2=576+324=900\) (Δ ABH vuông tại H)
\(\Rightarrow AB=30\left(cm\right)\)
\(AC^2=AH^2+CH^2=576+1024=1600\) (Δ ACH vuông tại H)
\(\Rightarrow AC=40\left(cm\right)\)
Xét tam giác AHB vuông tại H có:
AH2+HB2=AB2(định lý pythagore) (1)
Xét tam giác AHC vuông tại H có:
HA2+HC2=AC2 (định lý pythagore) (2)
Từ (1) và (2) ta cộng lại vế theo vế, có:
2AH2+BH2+CH2=AB2+AC2
<=>2AH2+BH2+CH2=BC2
<=> 2AH2+182+322=(18+32)2
<=>2AH2+1348=2500
<=>2AH2=2500-1348
<=>2AH2=1152
<=>AH2=1152:2
<=>AH2=576
<=>AH=\(\sqrt{576}\)
<=>AH=24(cm)
-Ta thay AH=24cm vào (1) ta có:
HB2+AH2=AB2
<=>182+242=AB2
<=>900=AB2
<=>\(AB=\sqrt{900}=30\)(cm)
-Ta thay AH=24cm vào (2) ta có:
HC2+HA2=AC2
<=>322+242=AC2
<=>1600=AC2
\(\Leftrightarrow AC=\sqrt{1600}=40\left(cm\right)\)
Vậy AB=30cm; AC=40cm

Bài 3 :
\(BC=HC+HB=16+9=25\left(cm\right)\)
\(BC^2=AB^2+AC^2\Rightarrow AB^2=BC^2-AC^2=25^2-20^2=625-400=225=15^2\)
\(\Rightarrow AB=15\left(cm\right)\)
\(AH^2=HC.HB=16.9=4^2.3^2\Rightarrow AH=3.4=12\left(cm\right)\)
Bài 6:
\(AB=AC=4\left(cm\right)\) (Δ ABC cân tại A)
\(BH=HC=2\left(cm\right)\) (Ah là đường cao, đường trung tuyến cân Δ ABC)
\(BC=BH+HC=2+2=4\left(cm\right)\)
Chu vi Δ ABC :
\(4+4+4=12\left(cm\right)\)

a) Chứng minh : BHCK là hình bình hành
Xét tứ giác BHCK có : MH = MK = HK/2
MB = MI = BC/2
Suy ra : BHCK là hình bình hành
b) BK vuông góc AB và CK vuông góc AC
Vì BHCK là hình bình hành ( cmt )
Suy ra : BK // HC và CK // BH ( tính chất hình bình hành )
mà CH vuông góc AB = F và BH vuông góc AC = E ( gt )
Suy ra : BK vuông góc AB và CK vuông góc AC ( Từ vuông góc đến // )
c) Chứng minh : BIKC là hình thang cân
Vì I đối xứng với H qua BC nên BC là đường trung bình của HI
Mà M thuộc BC Suy ra : MH = MI ( tính chất đường trung trực )
mà MH = MK = HK/2 (gt)
Suy ra : MI = MH = MK = 1/2 HC
Suy ra : Tam giác HIK vuông góc tại I
mà BC vuông góc HI (gt)
Suy ra : IC // BC
Suy ra : BICK là hình thang (1)
Ta có : BC là đường trung trực của HI (cmt)
Suy ra : CI = CH
Tiếp ý c
mà CH = BK ( vì BKCH là hình bình hành)
Suy ra : BK = CI (2)
Từ ( 1) và (2) Suy ra : BICK là hình thang cân (dấu hiệu nhận biết )
d) Giả sử GHCK là hình thang cân
Suy ra : Góc HCK = Góc GHC
mà góc HCK + góc C1 = 90 độ
góc GHC + góc C2 = 90 độ
Suy ra : Góc C1= góc C2
Suy ra : CF là đường cao đồng thời là đường phân giác của tam giác ABC
Suy ra : Tam giác ABC cân tại C
\(AB^2=AH^2+BH^2\Rightarrow AH^2=AB^2-BH^2\left(1\right)\left(Pitago\right)\)
\(AC^2=AH^2+CH^2\Rightarrow AH^2=AC^2-CH^2\left(2\right)\left(Pitago\right)\)
\(\left(1\right),\left(2\right)\Rightarrow AC^2-CH^2=AB^2-BH^2\)
\(\Rightarrow AB^2+CH^2=AC^2+BH^2\)
\(\Rightarrow dpcm\)
Ta có \(AB^2-AC^2=\left(BH^2+AH^2\right)-\left(CH^2+AH^2\right)\) \(=BH^2-CH^2\) \(\Rightarrow AB^2+CH^2=AC^2+BH^2\), đpcm.
(Bài này kết quả vẫn đúng nếu không có điều kiện tam giác ABC vuông tại A.)