Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: BC=BH+CH
=4+6
=10(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH=\sqrt{4\cdot6}=2\sqrt{6}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB=\sqrt{4\cdot10}=2\sqrt{10}\left(cm\right)\\AC=\sqrt{6\cdot10}=2\sqrt{15}\left(cm\right)\end{matrix}\right.\)
b: M là trung điểm của AC
=>\(AM=\dfrac{AC}{2}=\sqrt{15}\left(cm\right)\)
Xét ΔAMB vuông tại A có
\(tanAMB=\dfrac{AB}{AM}=\sqrt{\dfrac{2}{3}}\)
=>\(\widehat{AMB}\simeq39^0\)
c: ΔABM vuông tại A có AK là đường cao
nên \(BK\cdot BM=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\left(2\right)\)
Từ (1) và (2) suy ra \(BK\cdot BM=BH\cdot BC\)

c: Xét ΔABM vuông tại A có AK là đường cao
nên \(BK\cdot BM=AB^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BK\cdot BM=BH\cdot BC\)

c: Xét ΔABM vuông tại A có AK là đường cao ứng với cạnh huyền BM
nên \(BK\cdot BM=AB^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BK\cdot BM=BH\cdot BC\)

a: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH^2=4\cdot6=24\)
=>\(AH=2\sqrt{6}\left(cm\right)\)
ΔAHC vuông tại H
=>\(HA^2+HC^2=AC^2\)
=>\(AC^2=24+36=60\)
=>\(AC=2\sqrt{15}\left(cm\right)\)
ΔAHB vuông tại H
=>\(AB^2=AH^2+HB^2=16+24=40\)
=>\(AB=2\sqrt{10}\left(cm\right)\)
b: BC=BH+CH=10cm
c: ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\left(1\right)\)
Xét ΔABM vuông tại A có AK là đường cao
nên \(BK\cdot BM=BA^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BC=BK\cdot BM\)

a: \(AH=2\sqrt{6}\left(cm\right)\)
\(AB=2\sqrt{10}\left(cm\right)\)
\(AC=2\sqrt{15}\left(cm\right)\)

a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AC^2=CH\cdot BC\\AB^2=BH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=2\sqrt{6}\left(cm\right)\\AC=2\sqrt{15}\left(cm\right)\\AB=2\sqrt{10}\left(cm\right)\end{matrix}\right.\)

1:
BC=BH+CH
=3,6+6,4
=10(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH=\sqrt{3.6\cdot6.4}=4.8\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=\sqrt{3.6\cdot10}=6\left(cm\right)\\AC=\sqrt{6.4\cdot10}=8\left(cm\right)\end{matrix}\right.\)
Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
=>\(\widehat{C}\simeq37^0\)
ΔABC vuông tại A nên \(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{B}\simeq90^0-37^0=53^0\)
2:
ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\left(1\right)\)
ΔABM vuông tại A có AD là đường cao
nên \(BD\cdot BM=BA^2\left(2\right)\)
Từ (1),(2) suy ra \(BH\cdot BC=BD\cdot BM\)

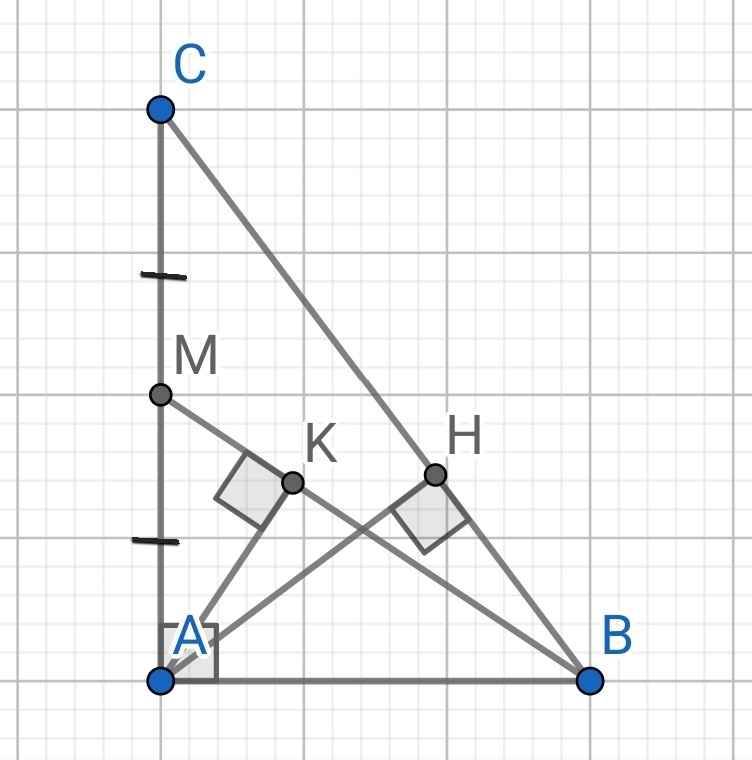
b: Xét ΔABM vuông tại A có AK là đường cao
nên \(BK\cdot BM=AB^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BK\cdot BM=BH\cdot BC\)
hay \(\dfrac{BK}{BH}=\dfrac{BC}{BM}\)
Xét ΔBKC và ΔBHM có
\(\dfrac{BK}{BH}=\dfrac{BC}{BM}\)
\(\widehat{MBH}\) chung
Do đó: ΔBKC\(\sim\)ΔBHM