Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: M là trung điểm của BC(gt)
nên \(BM=CM=\dfrac{BC}{2}=\dfrac{6}{2}=3cm\)
Ta có: ΔABC cân tại A(gt)
mà AM là đường trung tuyến ứng với cạnh đáy BC(M là trung điểm của BC)
nên AM là đường cao ứng với cạnh đáy BC(Định lí tam giác cân)
\(\Rightarrow AM\perp BC\)
Áp dụng định lí Pytago vào ΔABM vuông tại M, ta được:
\(AB^2=AM^2+BM^2\)
\(\Leftrightarrow AM^2=AB^2-BM^2=5^2-3^2=16\)
hay AM=4(cm)
Xét ΔABC có AM là đường cao ứng với cạnh BC(gt)
nên \(S_{ABC}=\dfrac{AM\cdot BC}{2}=\dfrac{4\cdot6}{2}=\dfrac{24}{2}=12cm^2\)
Vậy: Diện tích tam giác ABC là 12cm2
b) Xét tứ giác AMCN có
O là trung điểm của đường chéo AC(gt)
O là trung điểm của đường chéo MN(M và N đối xứng nhau qua O)
Do đó: AMCN là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành AMCN có \(\widehat{AMC}=90^0\)(\(AM\perp BC\))
nên AMCN là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
c) Hình chữ nhật AMCN trở thành hình vuông khi AM=CM
mà \(CM=\dfrac{BC}{2}\)(M là trung điểm của BC)
nên \(AM=\dfrac{BC}{2}\)
Xét ΔABC có
AM là đường trung tuyến ứng với cạnh BC(M là trung điểm của BC)
\(AM=\dfrac{BC}{2}\)(cmt)
Do đó: ΔABC vuông tại A(Định lí 2 về áp dụng hình chữ nhật vào tam giác vuông)
hay \(\widehat{BAC}=90^0\)
Vậy: Khi ΔABC có thêm điều kiện \(\widehat{BAC}=90^0\) thì AMCN là hình vuông

a.
AM là đường trung tuyến của tam giác ABC cân tại A
=> AM là đường cao của tam giác ABC cân tại A
=> AM _I_ BC
hay AMC = 900
I là trung điểm của AC (gt)
I là trung điểm của MN (M đối xứng N qua I)
=> AMCN là hình bình hành
mà AMC = 900
=> AMCN là hình chữ nhật
K là trung điểm của AB (gt)
M là trung điểm của BC (AM là đường trung tuyến của tam giác ABC)
=> KM là đường trung bình của tam giác ABC
=> KM = AC/2
mà IC = AC/2 (I là trung điểm của AC)
=> KM = IC
mà KM // IC (KM là đường trung bình của tam giác ABC)
=> MKIC là hình bình hành
b.
AN = MC (AMCN là hình chữ nhật)
mà MC = BM (M là trung điểm của BC)
=> AN = BM
mà AN // BM (AMCN là hình chữ nhật)
=> ANMB là hình bình hành
mà E là trung điển của AM
=> E là trung điểm của BN
c.
AMCN là hình vuông
<=> Tam giác ABC vuông cân tại A

a: Xét tứ giác ANMC có
MN//AC
MN=AC
Do đó: ANMC là hình bình hành

a) Tứ giác ANCM có hai đường chéo MN và AC cắt nhau tại H
mà H là trung điểm AC và H alf trung điểm MN
=> ANCM là hình bình hành
b) M là trung điểm BC, H là trung điểm AC => MH là đường trung bình của tam giác ABC
=> MH // AB mà AB \(\perp\)AC => MH\(\perp\)AC hay MN\(\perp\)AC
=> Hình bình hành ANCM là hình thoi
AB= 4cm , AC= 3cm, tam giác ABC vuông tại A
Áp dụng định lí Pi ta go
=> BC=5 cm
Tam giác ABC vuông tại A có AM là đường trung tuyến => AM=1/2BC=2,5 cm , Các cạnh của hình thoi bằng nhau và bằng 2,5 cm

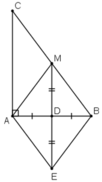
a) Ta có MB = MC, DB = DA
⇒ MD là đường trung bình của ΔABC
⇒ MD // AC
Mà AC ⊥ AB
⇒ MD ⊥ AB.
Mà D là trung điểm ME
⇒ AB là đường trung trực của ME
⇒ E đối xứng với M qua AB.
b) + MD là đường trung bình của ΔABC
⇒ AC = 2MD.
E đối xứng với M qua D
⇒ D là trung điểm EM
⇒ EM = 2.MD
⇒ AC = EM.
Lại có AC // EM
⇒ Tứ giác AEMC là hình bình hành.
+ Tứ giác AEBM là hình bình hành vì có các đường chéo cắt nhau tại trung điểm của mỗi đường.
Hình bình hành AEBM lại có AB ⊥ EM nên là hình thoi.
c) Ta có: BC = 4cm ⇒ BM = 2cm
Chu vi hình thoi AEBM bằng 4.BM = 4.2 = 8cm
d)- Cách 1:
Hình thoi AEBM là hình vuông ⇔ AB = EM ⇔ AB = AC
Vậy nếu ABC vuông có thêm điều kiện AB = AC (tức tam giác ABC vuông cân tại A) thì AEBM là hình vuông.
- Cách 2:
Hình thoi AEBM là hình vuông ⇔ AM ⊥ BM
⇔ ΔABC có trung tuyến AM là đường cao
⇔ ΔABC cân tại A.
Vậy nếu ΔABC vuông có thêm điều kiện cân tại A thì AEBM là hình vuông.

https://lazi.vn/edu/exercise/cho-tam-giac-abc-goi-d-e-f-theo-thu-tu-la-trung-diem-cua-ab-bc-ca-goi-m-n-p-q-theo-thu-tu-la-trung-diem
Bạn xem tại link này nhé
Học tốt!!!!!!

I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
a. Xét tam giác ABC có BM=MC; AI=IC
=> IM là đường trung bình của tam giác ABC => IM//AB; IM=1/2AB=AK
Xét tứ giác AKMI có IM//AK; IM=AK
=> AKMI là hbh
Do AB=AC=> 1/2AB=1/2AC=> AK=AI
Xét hbh AKMI có AK=AI
=> AKMI là hình thoi
b. •Xét tứ giác AMCN có AC, MN là 2 đường chéo cắt nhau tại I và AI=IC MI=IN
=> AMCN là hbh
Do tam giác ABC cân tại A nên AM vừa là trung tuyến vừa là đường cao
=> AMC=90*
Hbh AMCN có AMC=90*
=> AMCN là hcn
• Xét tam giác ABC có AK=BK; BM=MC
=> KM là đường trung bình của tam giác ABC => KM//AC hay KM//IC; KM=1/2AC=IC
Xét tứ giác MKIC có KM//IC; KM=IC
=> MKIC là hbh
c. Do AMCN là hcn nên NAM=90*; AN=MC
Từ NAM=90*=> ANvgAM mà BMvgAM
=> AN//BM
Từ AN=MC mà MC=BM => AN=BM
Xét tứ giác ABMN có AN=BM; AN//BM
=> ABMN là hbh => AM và BN cắt nhau tại trung điểm mỗi đoạn
Mà E là trung điểm của AM
=> E là trung điểm của BN
d. Để AMCN là hình vuông thì AC vg MN
Xét tam giác vuông AMC có MI vừa là trung tuyến vưaf là đường cao
=> AMC vuông cân tại M => ACM=45*=ABM
=> tam giác ABC vuông cân tại A
a: AM=BC/2=3cm
b: Xét tứ giác AMCN có
O là trung điểm chung của AC và MN
MA=MC
Do đó: AMCN là hình thoi