Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\tan\widehat{B}=\dfrac{AC}{AB}=\dfrac{5}{12}\Leftrightarrow AC=\dfrac{5}{12}\cdot6=2,5\left(cm\right)\\ b,BC=\sqrt{AC^2+AB^2}=\sqrt{2,5^2+6^2}=6,5\left(cm\right)\left(pytago\right)\)
a) Xét tam giác ABC vuông tại A:
\(AC=tan\alpha.AB=\dfrac{5}{12}.6=2,5\left(cm\right)\)
b) Áp dụng đ/lý Pytago trong tam giác ABC vuông tại A:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{2,5^2+6^2}=6,5\left(cm\right)\)

a: ΔANB vuông tại N
=>tan B=AN/NB
=>AN=NB*tan38
ΔANC vuông tại N
=>AN=NC*tan30
=>NB*tan38=NC*tan30
=>NB/NC=tan30/tan38\(\simeq0,74\)
=>NB=0,74NC
mà NB+NC=11
nên \(NB\simeq4,68\left(cm\right);NC\simeq6,32\left(cm\right)\)
AN=NC*tan30=6,32*tan30\(\simeq3,65\left(cm\right)\)
b: góc BAC=180-38-30=180-68=112 độ
Xét ΔABC có BC/sinA=AC/sinB
=>\(AC=\dfrac{11}{sin112}\cdot sin38\simeq7,3\left(cm\right)\)

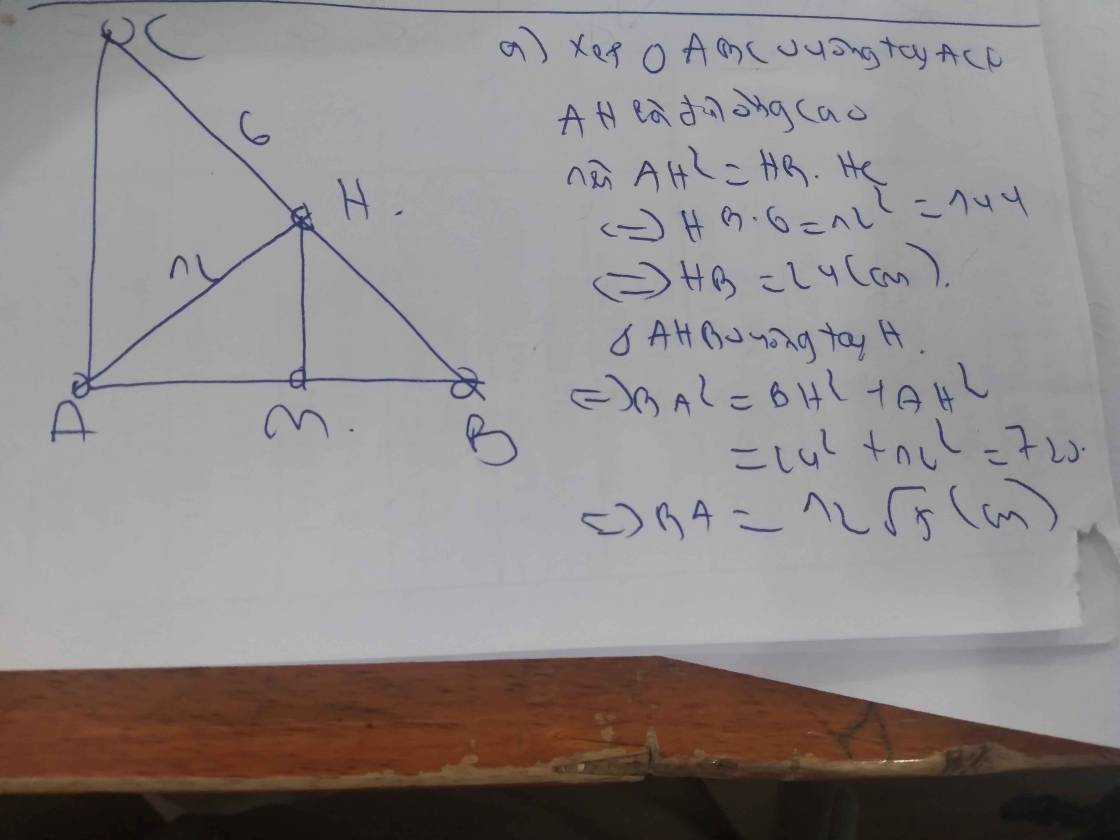
2: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(1\right)\)
Xét ΔBDC vuông tại B có BA là đường cao ứng với cạnh huyền DC
nên \(AD\cdot AC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BC=AD\cdot AC\)

a: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=4,8cm
Xét ΔABC vuông tại A có \(sinACB=\dfrac{AB}{BC}=\dfrac{3}{5}\)
=>\(\widehat{ACB}\simeq36^052'\)
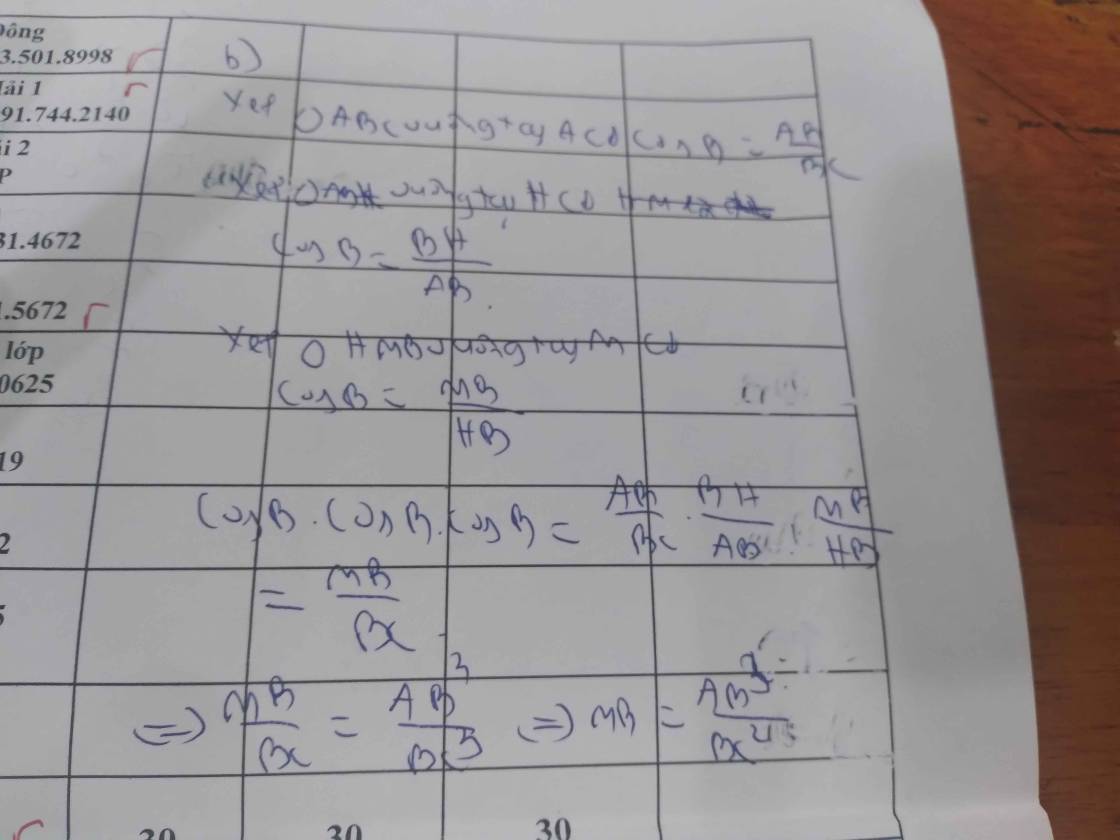
b: ΔHAB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
ΔHAC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1),(2) suy ra \(AE\cdot AB=AF\cdot AC\)
=>\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Do đó: ΔAEF đồng dạng với ΔACB
=>\(\widehat{AFE}=\widehat{ABC}\)

Bài 1:
a) Ta có:
\(tanB=\dfrac{AC}{AB}\Rightarrow\dfrac{AC}{AB}=\dfrac{5}{2}\)
\(\Rightarrow AC=\dfrac{AB\cdot5}{2}=\dfrac{6\cdot5}{2}=15\)
b) Áp dụng Py-ta-go ta có:
\(BC^2=AB^2+AC^2=6^2+15^2=261\)
\(\Rightarrow BC=\sqrt{261}=3\sqrt{29}\)
Bài 2:
\(\left\{{}\begin{matrix}sinM=sin40^o\approx0,64\Rightarrow cosN\approx0,64\\cosM=cos40^o\approx0,77\Rightarrow sinN\approx0,77\\tanM=tan40^o\approx0,84\Rightarrow cotN\approx0,84\\cotM=cot40^o\approx1,19\Rightarrow tanN\approx1,19\end{matrix}\right.\)
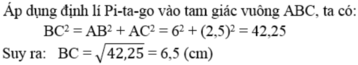

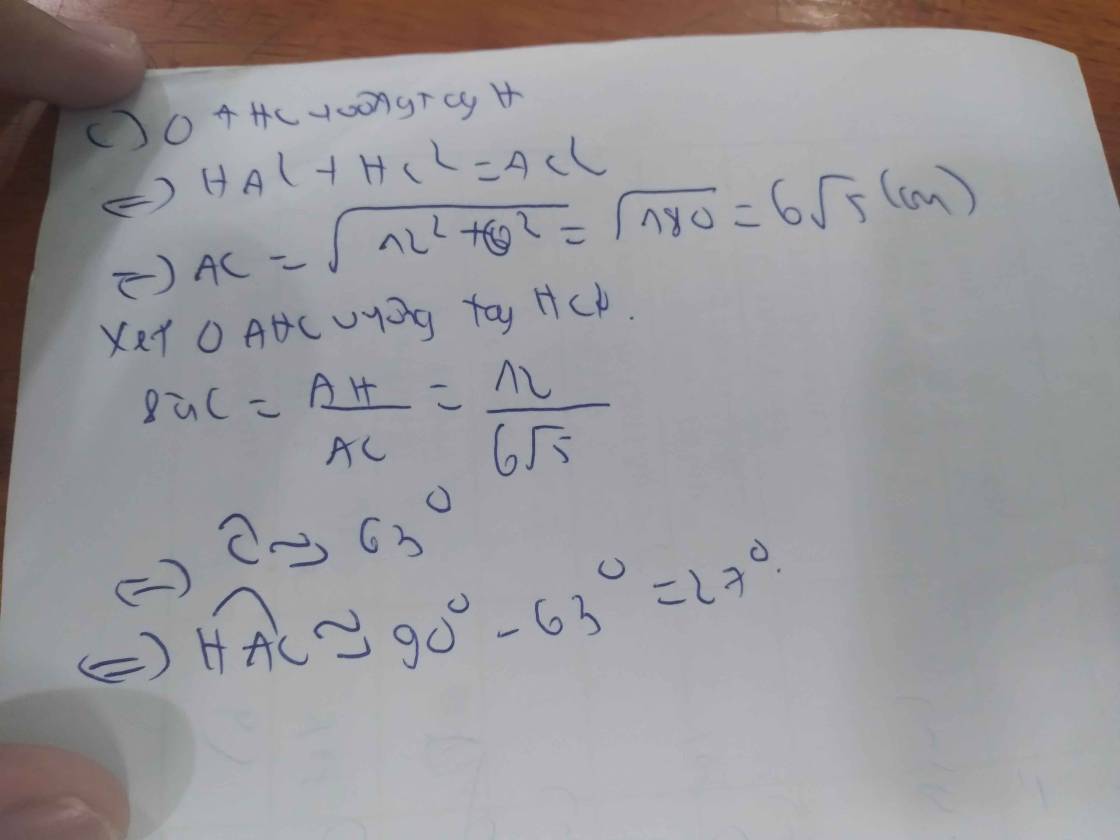
a, theo đề ta có : \(\frac{AC}{AB}\) = \(\frac{5}{12}\)
=> AC= 6.5:12=2,5
b, ta có: BC= \(\sqrt{AC^2+AB^2}\) = \(\frac{13}{2}\)