Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta dễ thấy tam giác KMN đồng dạng tam giác ABC (g.g)
\(\Rightarrow\frac{S_{KMN}}{S_{ABC}}=\left(\frac{MN}{BC}\right)^2\)
Vì \(S_{ABC}\) và \(MN\) không đổi nên \(S_{KMN}\) đạt giá trị nhỏ nhất khi MN đạt giá trị nhỏ nhất. Khi đó MN sẽ trùng với đường trung bình PQ trên hình vẽ . Vậy \(minS_{KMN}=\frac{1}{4}S_{ABC}\Leftrightarrow MN=PQ\)

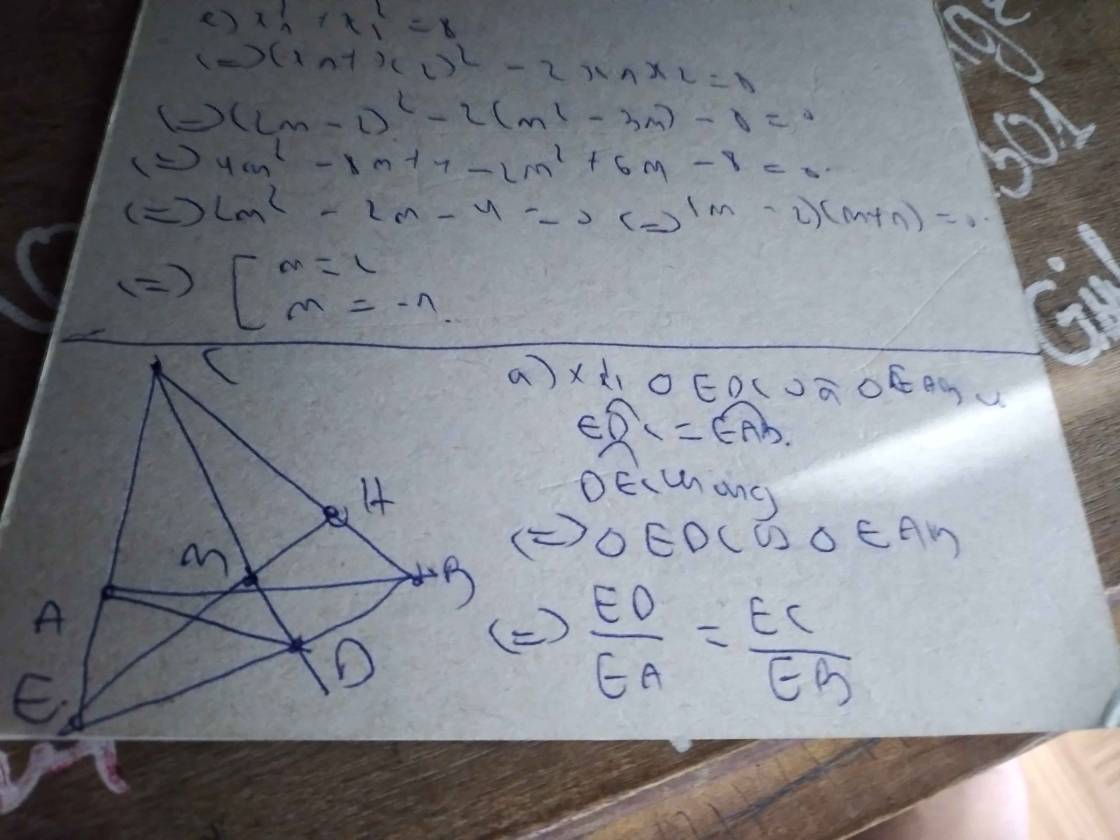
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
góc BAD chung
=>ΔABD=ΔACE
b: ΔABD=ΔACE
=>góc ABD=góc ACE
=>góc HBC=góc HCB
=>ΔHBC cân tại H
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC

a/
Ta có
\(\widehat{BAE}+\widehat{DAE}=\widehat{ABC}=90^o\)
\(\widehat{FAD}+\widehat{DAE}=\widehat{FAE}=90^o\)
\(\Rightarrow\widehat{BAE}=\widehat{FAD}\)(1)
Ta có \(AB=AD\) (2)
Xét tg vuông BAE và tg vuông DAF
Từ (1) và (2) \(\Rightarrow\Delta BAE=\Delta DAF\) (hai tg vuông có cạnh góc vuông và góc nhọn tương ứng bằng nhau)
\(\Rightarrow AE=AF\Rightarrow\Delta AEF\) cân tại A
Mà \(\widehat{FAE}=90^o\Rightarrow\Delta AEF\) vuông cân tại A
Xét \(\Delta AEF\) có
IE=IF
\(\Rightarrow AD\perp EF\) (trong tg cân đường trung tuyến xp từ đỉnh đồng thời là đường cao)
Xét \(\Delta KEF\) có
IE=IF; \(AD\perp EF\)
\(\Rightarrow\Delta KEF\) là tg cân (trong tg đường cao xp từ đỉnh đồng thời là đường trung tuyến thì tg đó là tg cân) \(\Rightarrow KE=KF\)
b/
Ta có \(\Delta AEF\) vuông cân tại A \(\Rightarrow\widehat{AFE}=\widehat{AEF}=45^o\) (1)
Xét \(\Delta ABD\) có
AB=AD; \(\widehat{BAD}=90^o\Rightarrow\Delta ABD\) vuông cân tại A \(\Rightarrow\widehat{ADB}=\widehat{ABD}=45^o\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{ADB}=\widehat{AEF}\) (3)
Gọi P là giao của AD với EF; Q là giao của BD với AE
Xét \(\Delta AFP\) và \(\Delta ABQ\) có
AD=AB
\(\Delta AEF\) cân tại A => AF=AE
\(\widehat{DAF}=\widehat{BAE}\left(cmt\right)\)
\(\Rightarrow\Delta AFP=\Delta ABQ\left(c.g.c\right)\Rightarrow\widehat{APF}=\widehat{AQB}\)
Mà \(\widehat{APF}=\widehat{DPI};\widehat{AQB}=\widehat{EQI}\) (góc đối đỉnh)
\(\Rightarrow\widehat{DPI}=\widehat{EQI}\) (4)
Nối D với I, B với I. Xét \(\Delta DPI\) và \(\Delta EQI\)
Từ (3) và (4) \(\Rightarrow\widehat{DIP}=\widehat{EIQ}\)
Mà \(\widehat{EIQ}+\widehat{FIB}=\widehat{FIE}=180^o\)
\(\Rightarrow\widehat{DIP}+\widehat{FIB}=\widehat{DIB}=180^o\) => D; I; B thẳng hàng
c/
Ta có \(AM=AB-BM;CE=BC-BE\)
Mà \(BM=BE;AB=BC\)
\(\Rightarrow AM=CE\)
Ta có AD=CD
\(S_{\Delta ADM}=\frac{AD.AM}{2}=S_{\Delta CDE}=\frac{CD.CE}{2}\Rightarrow S_{\Delta ADM}+S_{\Delta CDE}=2S_{\Delta CDE}=CD.CE\)
\(S_{\Delta BME}=\frac{BE.BM}{2}=\frac{BE^2}{2}\)
Gọi a là cạnh hình vuông ABCD có
\(S_{\Delta DEM}=S_{ABCD}-\left(S_{\Delta ADM}+S_{\Delta CDE}+S_{BME}\right)=\)
\(=a^2-2S_{\Delta CDE}-\frac{BE^2}{2}=a^2-a.CE-\frac{\left(a-CE\right)^2}{2}=\)
\(=\frac{2a^2-2a.CE-a^2+2a.CE-CE^2}{2}=\frac{a^2-CE^2}{2}\)
\(\Rightarrow S_{\Delta DEM}\) lớn nhất khi \(a^2-CE^2\) lớn nhất \(\Rightarrow CE^2\) nhỏ nhất => CE nhỏ nhất
CE nhỏ nhất khi CE=0 => E trùng C