
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



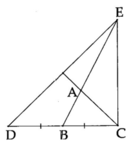
a) Ta có BD = BC, do đó EB là đường trung tuyến của tam giác CDE .
Mặt khác AE = 2AB nên A là trọng tâm của tam giác CDE.
b) Vì A là trọng tâm của tam giác CDE nên CA là đường trung tuyến, suy ra ĐPCM

a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
Do đo: ΔBAD=ΔBED
=>DA=DE
b,c: Xét ΔBFC có BA/AF=BE/EC
nên AE//FC
BA=BE
DA=DE
Do đó; BD là trung trực của AE
=>BD vuông góc với AE
=>BD vuông góc với FC
d: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
góc ADF=góc EDC
Do đó: ΔDAF=ΔDEC
=>góc ADF=góc EDC
=>góc ADF+góc ADE=180 độ
=>D,E,F thẳng hàng

https://olm.vn/hoi-dap/detail/204652944487.html tham khao nha
A,Xét \(\Delta AME\)và\(\Delta DMB\)có
AM=DM (gt)
BM=EM (gt)
AME^=DMB^ (đối đỉnh)
\(=>\Delta AME=\Delta DMB\left(c-g-c\right)\)
\(=>AE=BD\)
B,Xét \(\Delta AMF\)và \(\Delta DMC\)có:
\(DM=AM\left(gt\right)\)
\(CM=FM\left(gt\right)\)
AMF^=CMC^(Đối đỉnh)
\(=>\Delta AMF=\Delta DMC\left(c-g-c\right)\)
=>FAM^=CDM^
Do 2 góc này = nhau và ở vị trí sole
\(=>AF//DC\)
C,theo câu A ta có : EAM^=BDM^
=>AE//BD
theo câu B ta có :
AF//DC