Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tứ giác BCEF có
\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)
nên BCEF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Tâm I của đường tròn ngoại tiếp tứ giác BCEF là trung điểm của BC
bạn tham khảo ở đây nha,bài này mình từng làm rồi
https://hoc24.vn/cau-hoi/881cho-tam-giac-abc-nhon-noi-tiep-duong-tron-o-cac-duong-cao-adbecf-cat-nhau-tai-ha-chung-minh-tu-giac-bcef-noi-tiep-va-xac-dinh-tam-i-cua-duong-tron-ngoai-tiep-tu-giacb-duong-thang-ef-cat-duon.1092906662181

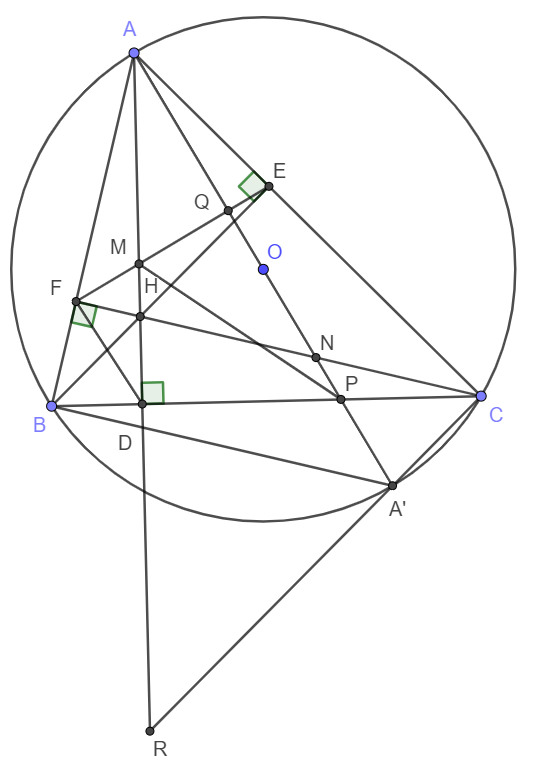
a) theo gt, BFC=BEC=90
=> BFEC nội tiếp (có 2 góc kề bang nhau)
góc AFC=ADC=90 => AFDC nội tiếp ( có 2 cạnh kề cùng nhìn một đoan thẳng bằng nhau)
b) vì tứ giác ABA'C nội tiếp => ABC = AA'C (cùng chắn cung AC)
Lại có ABC= AHF (Cùng phụ với góc BAD)
Ta thấy AFHE nội tiếp vì AFH +AEH = 90+90=180
=> AHF=AEF (Cùng chắn cung AF)
=>Đpcm
c) vì tứ giác EQA'C nôi tiếp
nên EQA'+ECA'=180 mà ECA'=90 vì là góc nội tiếp chắn nửa đường tròn
=> MQP=EQA'=90 ( vì MQP+EQA=180)
Trong đó ADC=90 =>Đpcm
d) Vì ABA'C VÀ FBDH nội tiếp nên góc NA'C=ABC=DHC
=>NA'C=DHC=>Đpcm

a) Ta có: \(\angle BFC=\angle BEC=90\Rightarrow BCEF\) nội tiếp
Gọi I là trung điểm BC
Ta có: \(\Delta BFC\) vuông tại F có I là trung điểm BC \(\Rightarrow IF=IB=IC\)
\(\Delta BEC\) vuông tại E có I là trung điểm BC \(\Rightarrow IE=IB=IC\)
\(\Rightarrow IE=IF=IB=IC\Rightarrow I\) là tâm (BCEF)
b) Xét \(\Delta MKB\) và \(\Delta MCT:\) Ta có: \(\left\{{}\begin{matrix}\angle MKB=\angle MCT\left(BKTCnt\right)\\\angle TMCchung\end{matrix}\right.\)
\(\Rightarrow\Delta MKB\sim\Delta MCT\left(g-g\right)\Rightarrow\dfrac{MK}{MC}=\dfrac{MB}{MT}\Rightarrow MK.MT=MB.MC\left(1\right)\)
Xét \(\Delta MFB\) và \(\Delta MCE:\) Ta có: \(\left\{{}\begin{matrix}\angle MFB=\angle MCE\left(BCEFnt\right)\\\angle EMCchung\end{matrix}\right.\)
\(\Rightarrow\Delta MFB\sim\Delta MCE\left(g-g\right)\Rightarrow\dfrac{MF}{MC}=\dfrac{MB}{ME}\Rightarrow MB.MC=MF.ME\left(2\right)\)
Ta có: \(\angle AFC=\angle ADC=90\Rightarrow AFDC\) nội tiếp
Tương tự \(\Rightarrow ABDE,AEHF\) nội tiếp
Ta có: \(\angle FEI=\angle FEB+\angle BEI=\angle FAH+\angle EBI\) (\(\Delta EBI\) cân tại I)
\(=\angle FAH+\angle EAD=\angle BAC=\angle BDF\) (AFDC nội tiếp)
\(\Rightarrow FDIE\) nội tiếp \(\Rightarrow\angle MDF=\angle MEI\)
Xét \(\Delta MFD\) và \(\Delta MIE:\) Ta có: \(\left\{{}\begin{matrix}\angle MDF=\angle MEI\\\angle EMIchung\end{matrix}\right.\)
\(\Rightarrow\Delta MFD\sim\Delta MIE\left(g-g\right)\Rightarrow\dfrac{MF}{MI}=\dfrac{MD}{ME}\Rightarrow MD.MI=MF.ME\left(3\right)\)
Từ (1),(2) và (3) \(\Rightarrow MD.MI=MK.MT\)
c) Từ C kẻ đường thẳng song song với NS cắt AB,AD lần lượt tại J và L
Vì \(CJ\parallel NS\) và \(NS\bot IH\Rightarrow CJ\bot IH\) mà \(CD\bot HL\)
\(\Rightarrow I\) là trực tâm tam giác CHL \(\Rightarrow LI\bot HC\) mà \(AJ\bot CH\)
\(\Rightarrow IL\parallel BJ\) mà I là trung điểm BC \(\Rightarrow L\) là trung điểm CJ
mà \(CJ\parallel NS\) \(\Rightarrow G\) là trung điểm NS (dùng Thales để biến đổi thôi,bạn tự chứng minh nha)

a: Xét tứ giác BDEA có
góc BDA=góc BEA=90 độ
=>BDEA là tứ giác nội tiếp
b: Kẻ tiếp tuyến Ax
=>góc xAC=góc ABC
mà góc ABC=góc AEF(=180 độ-góc FEC)
nên góc xAC=góc AEF
=>Ax//FE
=>FE vuông góc OA
Xét (O) có
ΔACA' nội tiếp
AA' là đường kính
=>ΔACA' vuông tại C
Xét tứ giác A'CEM có
góc EMA'+góc ECA'=180 độ
=>A'CEM là tứ giác nội tiếp

a: góc HDC+góc HEC=180 độ
=>HDCE nội tiếp
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
c: góc AFH+góc AEH=180 độ
=>AEHF nội tiếp
góc FEH=góc BAD
góc DEH=góc FCB
mà góc BAD=góc FCB
nên góc FEH=góc DEH
=>EH là phân giác của góc DEF

a) Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)
nên BFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{BAE}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC(g-g)
Suy ra: \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
hay \(AE\cdot AC=AB\cdot AF\)

a: góc BDH+góc BFH=180 độ
=>BDHF nội tiếp
góc BFC=góc BEC=90 dộ
=>BFEC nội tiếp
b: góc FEB=góc BAD
góc DEB=góc FCB
mà góc BAD=góc FCB
nên góc FEB=góc DEB
=>EB là phân giác của góc FED
c: Kẻ tiếp tuyến Ax của (O)
=>góc xAC=góc ABC=góc AEF
=>Ax//FE
=>FE vuông góc OA
=>OA vuông góc IK