Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{EAB}\) chung
Do đó: ΔAEB đồng dạng với ΔAFC
=>\(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
=>\(AE\cdot AC=AB\cdot AF\)
2: Xét tứ giác BFHD có \(\widehat{BFH}+\widehat{BDH}=90^0+90^0=180^0\)
nên BFHD là tứ giác nội tiếp
=>\(\widehat{FBH}=\widehat{FDH}\)
=>\(\widehat{FDH}=\widehat{ABE}\left(1\right)\)
Xét tứ giác CEHD có
\(\widehat{CEH}+\widehat{CDH}=90^0+90^0=180^0\)
=>CEHD là tứ giác nội tiếp
=>\(\widehat{EDH}=\widehat{ECH}\)
=>\(\widehat{EDH}=\widehat{ACF}\left(2\right)\)
ΔABE đồng dạng với ΔACF
=>\(\widehat{ABE}=\widehat{ACF}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\widehat{FDH}=\widehat{EDH}\)
=>DH là phân giác của góc EDF

1: Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó: BFEC là tứ giác nội tiếp
Xét tứ giác AEDB có
\(\widehat{AEB}=\widehat{ADB}=90^0\)
Do đó: AEDB là tứ giác nội tiếp
2: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{EAB}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC
Suy ra: AE/AF=AB/AC
hay \(AE\cdot AC=AB\cdot AF\)

a: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
góc CDH+góc CEH=90+90=180 độ
=>CDHE nội tiếp
b: góc AFH+góc AEH=180 độ
=>AFHE nội tiếp
góc FEH=góc BAD
góc DEH=góc FCB
mà góc BAD=góc FCB
nên góc FEH=góc DEH
=>EH là phân giác của góc FED
Xét ΔBFE và ΔDHE có
góc BEF=góc DEH
góc BFE=góc DHE
=>ΔBFE đồng dạng với ΔDHE

a: Xét tứ giác AEHF có
\(\widehat{AEH}+\widehat{AFH}=180^0\)
Do đó: AEHF là tứ giác nội tiép
b: Xét tứ giác ABDE có
\(\widehat{AEB}=\widehat{ADB}=90^0\)
Do đó:ABDE là tứ giác nội tiếp
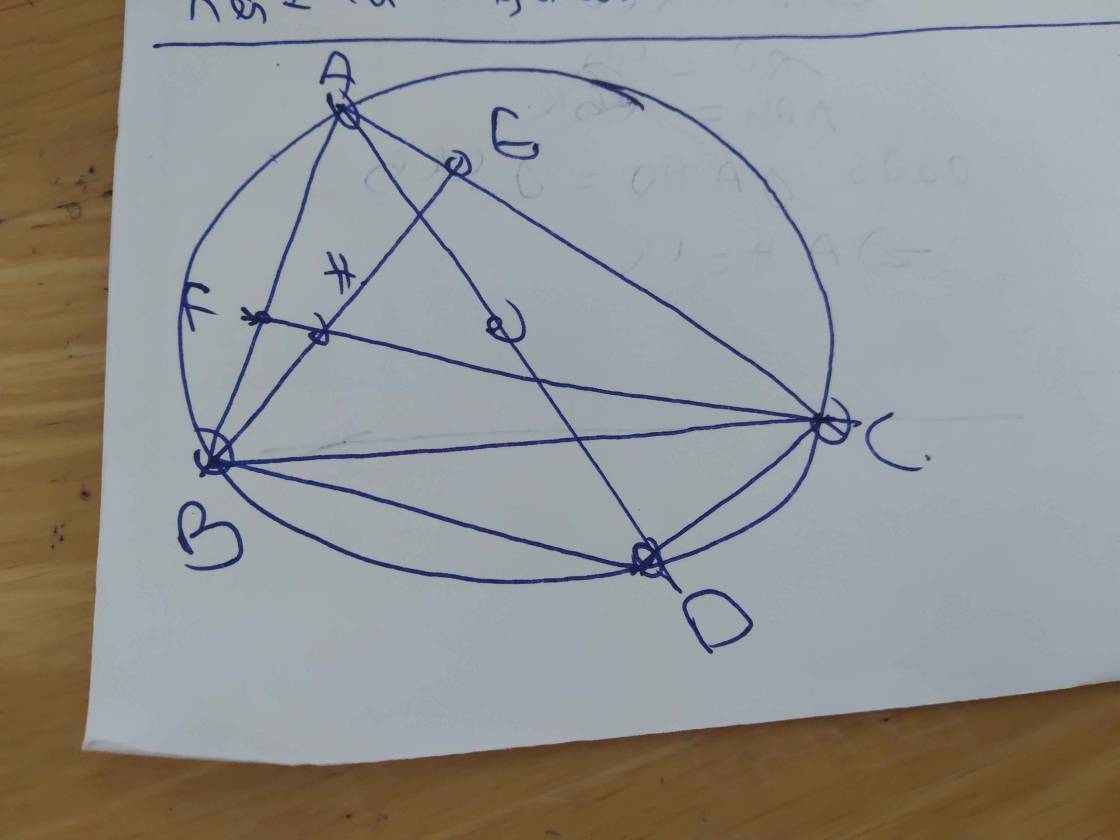


Bạn tự vẽ hình nhá
a,
CF , BE là các đường cao của tam giác ABC
=> CF vuông góc vs AB và BE vg với AC
=> Góc CFA = 90 độ và góc BEA = 90 độ
Xét tam giác ACF và tam giác ABE có :
Góc CAB chung
Góc CFA = góc BEA = 90 độ
=> Tam giác ACF đồng dạng vs tam giác ABE
=> AC / AB = AF / AE
<=> AC . AE = AF . AB ( đpcm)
b,
Chứng minh tứ giác CDHE nội tiếp ( tổng 2 góc đối = 180 độ )
=> Góc ECH = góc EDH ( 2 góc nt cùng chắn cung EH của đtr ngoại tiếp tg CDHE ) ( 1 )
C/m tứ giác DHFB nt ( tổng 2 góc đối = 180 độ )
=> Góc HDF = góc HBF ( 2 góc nt cùng chắn cung HF của đtr ngoại tiếp tg DHFB ) ( 2 )
Lại có : Tam giác ACF đồng dạng với tam giác ABE ( cmt )
=> Góc ACF = góc ABE
Hay góc ECH = góc HBF ( 3 )
Từ ( 1 ) , ( 2 ) , ( 3 ) => Góc EDH = góc FDH
Chứng tỏ DH là phân giác góc EDF ( đpcm)
c,
Chưa nghĩ đc