K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

25 tháng 3 2021
a) Xét tứ giác AEHF có
\(\widehat{AFH}\) và \(\widehat{AEH}\) là hai góc đối
\(\widehat{AFH}+\widehat{AEH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: AEHF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

1 tháng 2 2023
a: Xét tứ giác AEHF có
góc AEH+góc AFH=180 độ
=>AEHF là tứ giác nội tiếp
Xét tứ giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC là tứ giác nội tiếp
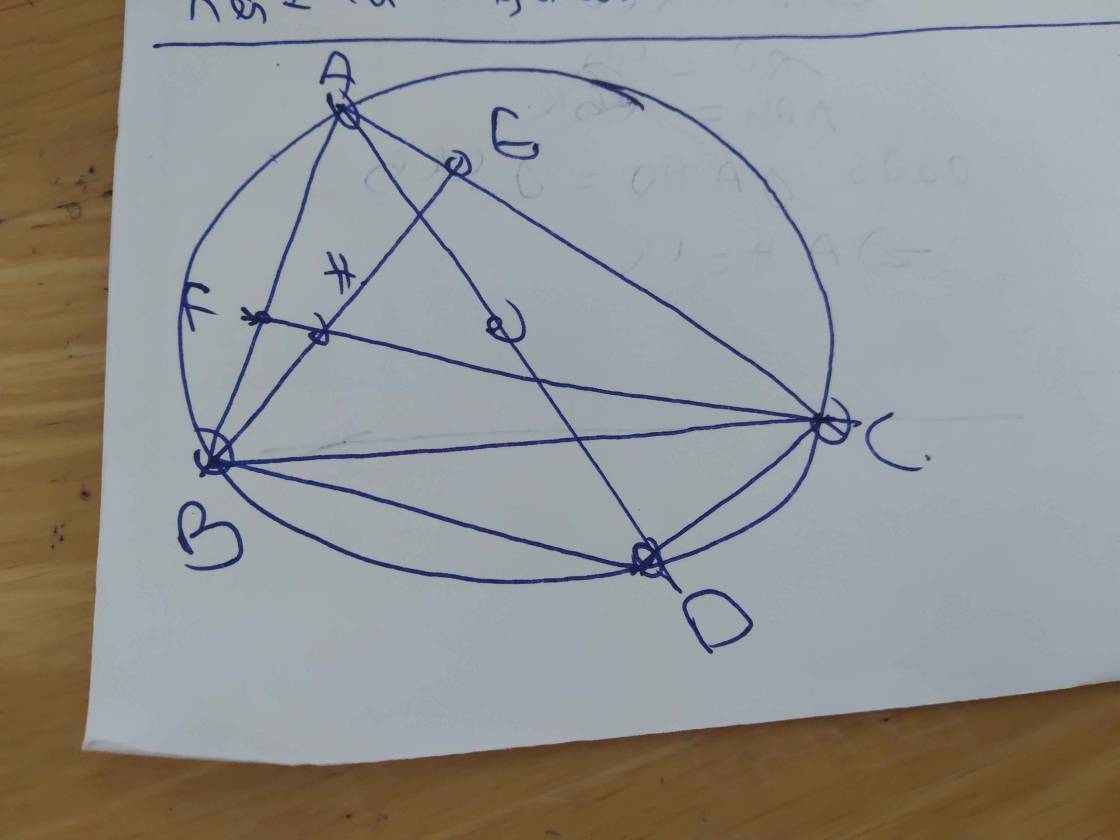
b: Xét (O) có
ΔABK nội tiếp
AK là đường kính
=>ΔABK vuông tại B
=>BK//CH
Xét (O) có
ΔACK nội tiếp
AK là đường kính
=>ΔACK vuông tại C
=>CK//BH
Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
=>I là trung điểm của BC


1: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{EAB}\) chung
Do đó: ΔAEB đồng dạng với ΔAFC
=>\(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
=>\(AE\cdot AC=AB\cdot AF\)
2: Xét tứ giác BFHD có \(\widehat{BFH}+\widehat{BDH}=90^0+90^0=180^0\)
nên BFHD là tứ giác nội tiếp
=>\(\widehat{FBH}=\widehat{FDH}\)
=>\(\widehat{FDH}=\widehat{ABE}\left(1\right)\)
Xét tứ giác CEHD có
\(\widehat{CEH}+\widehat{CDH}=90^0+90^0=180^0\)
=>CEHD là tứ giác nội tiếp
=>\(\widehat{EDH}=\widehat{ECH}\)
=>\(\widehat{EDH}=\widehat{ACF}\left(2\right)\)
ΔABE đồng dạng với ΔACF
=>\(\widehat{ABE}=\widehat{ACF}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\widehat{FDH}=\widehat{EDH}\)
=>DH là phân giác của góc EDF