HH
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HH
0
CM
12 tháng 10 2019
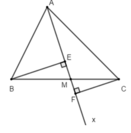
Vì BE ⊥ Ax tại E nên tam giác BEM vuông tại E ⇒ BM > BE (quan hệ đường xiên và đường vuông góc)
Vì CF ⊥ Ax tại F nên tam giác CFM vuông tại F ⇒ CM > CF (quan hệ đường xiên và đường vuông góc)
Khi đó ta có: BM + CM > BE + CF
Mà BM + CM = BC (M thuộc BC)
Do đó: BC > BE + CF hay BE + CF < BC.
Chọn đáp án A
DT
2. Cho tam giác ABC nhọn. D thuộc AC, E và F là hình chiếu của A và C xuống BD. So sánh AC với AE+CF
1
14 tháng 3 2021
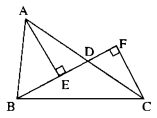
Xét ∆ADE vuông tại E có AD là cạnh huyền:
\(\Rightarrow\) AE < AD (1)
Xét ∆CFD vuông tại F có DC là cạnh huyền
\(\Rightarrow\) FC < DC (2)
Từ (1) và (2), suy ra:
AE + FC < AD + DC
hay AE + FC < AC
KN
24 tháng 1 2020
Theo giả thiết ta có: \(CF\perp AM\)nên \(\Delta MCF\)vuông tại F
Suy ra CF < MC (cạnh góc vuông bé hơn cạnh huyền) (1)
Tương tự ta có: BE < BM (2)
Từ (1) và (2) suy ra \(BE+CF< BM+MC=BC\)
Vậy \(BE+CF< BC\left(đpcm\right)\)
6 tháng 8 2018
Xét tam giác BEM và tam giác CFM có :
BM = MC ( gt )
Góc E = Góc F ( = 90độ )
Góc M1 = Góc M2 ( đối đính )
=> Tam giác BEM = tam giác CFM ( ch - gn )
=> BE = CF ( 2 cạnh tương ứng )
Vậy,..........