Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔFBC vuông tại F và ΔECB vuông tại E có
BC chung
góc FBC=góc ECB
Do đó: ΔFBC=ΔECB
=>CF=EB
b: Xét ΔMBC có góc MBC=góc MCB
nên ΔMCB cân tại M
=>MB=MC
mà AB=AC
nên AM là trung trực của BC

a) Vì \(\Delta ABC\) cân tại A nên AB = AC và Góc B = Góc C. Vì \(BE\perp AC;CF\perp AB\left(gt\right)\)
Nên ^AFC = ^BFC = ^AEB = ^CEB = 900. Xét \(\Delta AFC\) và \(\Delta AEB\) có :
^AFC = ^AEB = 900; \(AC=AB\left(cmt\right)\); Góc O chung. \(\Rightarrow\Delta AFC=\Delta AEB\left(ch.gn\right)\)
b) \(\Rightarrow AF=AE\) ( 2 cạnh tương ứng ). Có ^AFC = ^AEB hay ^AFD = ^AED = 900
Xét \(\Delta AED\) và \(\Delta AFD\) có : ^AFD = ^AED = 900 ( cmt ) ; \(AF=AE\left(cmt\right);AD\) chung
\(\Rightarrow\Delta AED=\Delta AFD\left(ch.cgv\right)\Rightarrow\) ^EAD = ^FAD ( tương ứng ) nên AD là phân giác ^FAE ( đpcm )
c) Gọi giao điểm của AM và DE tại N. Xét \(\Delta AEN\) và \(\Delta AFN\) có :
\(AE=AF\left(cmt\right)\); ^EAN = ^FAN ( ^EAD = ^FAD ); \(AN\) chung.
\(\Rightarrow\Delta AEN=\Delta AFN\left(c.g.c\right)\Leftrightarrow\) ^ANE = ^ANF ( tương ứng ). Mà ^ANE + ^ANF = 1800 ( kề bù )
=> ^ANE = ^ANF = 1800 : 2 = 900 \(\Leftrightarrow AN\perp FE\). Mà N là giao điểm của AM và FE
Nên N thuộc AM \(\Rightarrow AN\perp FE\Leftrightarrow AM\perp FE\left(đpcm\right)\)
Ờ ! viết bằng nhau ''='' thật đấy, nhưng trên hình kí hiệu j đâu mà viết nó ''='' nhau
LOGIC ?
Cái deck j vại, bn nhìn thấy ^O ở đâu thế bn Minh !
Ý thức ko mua đc ''='' tiền.

a) Xét ΔBEM vuông tại E và ΔCFM vuông tại F có
MB=MC(M là trung điểm của BC)
\(\widehat{BME}=\widehat{CMF}\)(hai góc đối đỉnh)
Do đó: ΔBEM=ΔCFM(cạnh huyền-góc nhọn)
b) Ta có: ΔBEM=ΔCFM(cmt)
nên BE=CF(hai cạnh tương ứng)
c) Xét ΔBMF và ΔCME có
MB=MC(M là trung điểm của BC)
\(\widehat{BMF}=\widehat{CME}\)(hai góc đối đỉnh)
MF=ME(ΔCFM=ΔBEM)
Do đó: ΔBMF=ΔCME(c-g-c)
⇒\(\widehat{BFM}=\widehat{CEM}\)(hai góc tương ứng)
mà \(\widehat{BFM}\) và \(\widehat{CEM}\) là hai góc ở vị trí so le trong
nên BF//CE(Dấu hiệu nhận biết hai đường thẳng song song)

a: Xet ΔABE vuông tại E và ΔACF vuông tại F có
AB=AC
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACF
b: Xét ΔAFM vuông tại F và ΔAEM vuông tại E có
AM chung
AF=AE
Do đó: ΔAFM=ΔAEM
Suy ra: \(\widehat{BAM}=\widehat{CAM}\)
hay AM là tia phân giác của góc BAC

a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
AB=AC
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACF
b: Xét ΔFBC vuông tại F và ΔECB vuông tại E có
FB=EC
FC=EB
BC chung
DO đó: ΔFBC=ΔECB
Suy ra: \(\widehat{ICB}=\widehat{IBC}\)
hay ΔBIC cân tại I
d: Ta có: AB=AC
nên A nằm trên đường trung trực của BC(1)
Ta có: IB=IC
nên I nằm trên đường trung trực của BC(2)
Ta có: MB=MC
nên M nằm trên đường trung trực của BC(3)
Từ (1), (2) và (3) suy ra A,M,I thẳng hàng

b) Xét ΔEBC vuông tại E và ΔFCB vuông tại F có
BC chung
\(\widehat{ECB}=\widehat{FBC}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔEBC=ΔFCB(cạnh huyền-góc nhọn)
Suy ra: \(\widehat{EBC}=\widehat{FCB}\)(hai góc tương ứng)
hay \(\widehat{IBC}=\widehat{ICB}\)
Xét ΔBIC có \(\widehat{IBC}=\widehat{ICB}\)(cmt)
nên ΔIBC cân tại I(Định lí đảo của tam giác cân)
a) Xét ΔABE vuông tại E và ΔACF vuông tại F có
AB=AC(ΔABC cân tại A)
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACF(Cạnh huyền-góc nhọn)
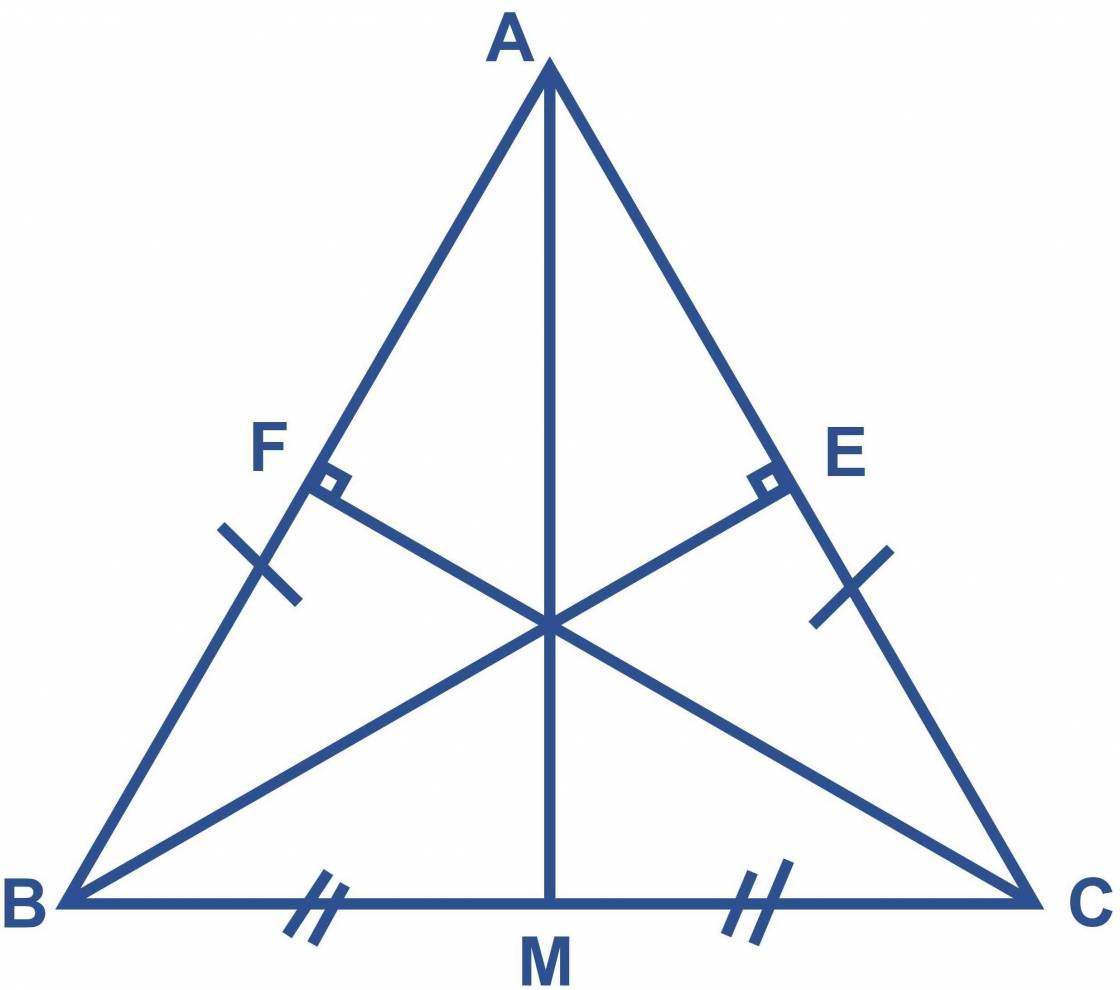
Xét tam giác BEM và tam giác CFM có :
BM = MC ( gt )
Góc E = Góc F ( = 90độ )
Góc M1 = Góc M2 ( đối đính )
=> Tam giác BEM = tam giác CFM ( ch - gn )
=> BE = CF ( 2 cạnh tương ứng )
Vậy,..........